浙江省2022年中考数学真题分类汇编05 二次函数

试卷更新日期：2022-07-03 类型：二轮复习

进入出卷网下载

一、单选题

1. 将抛物线y=x²向上平移3个单位，所得抛物线的解析式是（）

A、y=x²+3 B、y=x²-3 C、y=(x+3)² D、y=(x-3)²

查看试题解析
2. 点A (m-1，y₁)，B(m，y₂)都在二次函数y=(x-1)²+n的图象上。若y₁<y₂ ，则m的取值范围为（）

A、m>2 B、m> $\frac{3}{2}$ C、m<1 D、 $\frac{3}{2}$ <m<2

查看试题解析
3. 已知二次函数y=x²+ax+b(a，b为常数)．命题①：该函数的图象经过点(1，0)；命题②：该函数的图象经过点(3，0)；命题③：该函数的图象与x轴的交点位于y轴的两侧；命题④；该函数的图象的对称轴为直线x=1．如果这四个命题中只有一个命题是假命题，则这个假命题是（）

A、命题① B、命题② C、命题③ D、命题④

查看试题解析
4. 已知点 A（a，2）、B（b，2）、C（c，7）都在抛物线 $y = {(x - 1)}^{2} - 2$ 上，点A在点B左侧，下列选项正确的是（）

A、若 $c < 0$ ，则 $a < c < b$ B、若 $c < 0$ ，则 $a < b < c$ C、若 $c > 0$ ，则 $a < c < b$ D、若 $c > 0$ ，则 $a < b < c$

查看试题解析
5. 已知抛物线 y=x²+mx的对称轴为直线 x=2 ，则关于x的方程 x²+mx=5的根是（）

A、0，4 B、1，5 C、1，－5 D、－1，5

查看试题解析
6. 已知点A（a，b），B（4，c）在直线y＝kx＋3（k为常数，k≠0）上，若ab的最大值为9，则c的值为（）

A、1 B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析

二、综合题

7. 为了落实劳动教育，某学校邀请农科院专家指导学生进行小番茄的种植，经过试验，其平均单株产量y千克与每平方米种植的株数x（2≤x≤8，且x为整数）构成一种函数关系，每平方米种植2株时，平均单株产量为4千克；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量减少0.5千克．

(1)、求y关于x的函数表达式．

(2)、每平方米种植多少株时，能获得最大的产量？最大产量为多少下克？

查看试题解析
8. 设二次函数y₁=2x²+bx+c(b，c是常数)的图象与x轴交于A，B两点．

(1)、若A，B两点的坐标分别为(1，0)，(2，0)，求函数y)的表达式及其图象的对称轴．

(2)、若函数y₁的表达式可以写成心=2(x-h)²-2(h是常数)的形式，求b+c的最小值．

(3)、设一次函数y₂=x-m(m是常数)，若函数y₁的表达式还可以写成y₁=2(x-m)(x-m-2)的形式，当函数y=y₁-y₂的图象经过点(x₀ ， 0)时，求x₀-m的值．

查看试题解析
9. 已知函数y=-x²+bx+c（b，c为常数）的图象经过点（0，﹣3），（﹣6，﹣3）．

(1)、求b，c的值．

(2)、当﹣4≤x≤0时，求y的最大值．

(3)、当m≤x≤0时，若y的最大值与最小值之和为2，求m的值．

查看试题解析
10. 如图，已知点M（x₁ ， y₁），N（x₂ ， y₂）在二次函数y＝a（x﹣2）²﹣1（a＞0）的图象上，且x₂﹣x₁＝3．

(1)、若二次函数的图象经过点（3，1）.
①求这个二次函数的表达式；

②若y₁＝y₂ ，求顶点到MN的距离；

(2)、当x₁≤x≤x₂时，二次函数的最大值与最小值的差为1，点M，N在对称轴的异侧，求a的取值范围.

查看试题解析
11. 已知抛物线L₁：y＝a(x＋1)²－4（a≠0）经过点A（1，0）．

(1)、求抛物线L₁的函数表达式．

(2)、将抛物线L₁向上平移m（m＞0）个单位得到抛物线L₂ ．若抛物线L₂的顶点关于坐标原点O的对称点在抛物线L₁上，求m的值．

(3)、把抛物线L₁向右平移n（n＞0）个单位得到抛物线L₃ ，若点B（1，y₁），C（3，y₂）在抛物线L₃上，且y₁＞y₂ ，求n的取值范围．

查看试题解析
12. 已知抛物纸L₁：y=a(x+1)²-4(a≠0)经过点A(1，0)。

(1)、求抛物线L₁的函数表达式。

(2)、将抛物线L₁向上平移m(m>0)个单位得到抛物线L₂ ，若抛物线L₂的顶点关于坐标原点O的对称点在抛物线L₁上，求m的值．

(3)、把抛物线L₁向右平移n(n>0)个单位得到抛物线L₃ ，已知点P(8-t，s)，Q(t-4，r)都在抛物线L₃上，若当t>6时，都有s>r，求n的取值范围．

查看试题解析
13. 如图1，灌溉车沿着平行于绿化带底部边线l的方向行驶，为绿化带浇水．喷水口H离地竖直高度为h（单位： m）．如图2，可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象；把绿化带横截面抽象为矩形 DEFG ，其水平宽度DE=3m，竖直高度为EF的长．下边缘抛物线是由上边缘抛物线向左平移得到，上边缘抛物线最高点A离喷水口的水平距离为2m，高出喷水口0.5m，灌溉车到l 的距离OD为d（单位：m）．

(1)、若h=1.5，EF=0.5m；
①求上边缘抛物线的函数解析式，并求喷出水的最大射程 OC；

②求下边缘抛物线与x 轴的正半轴交点B的坐标；

③要使灌溉车行驶时喷出的水能浇灌到整个绿化带，求d的取值范围；

(2)、若 EF=1m．要使灌溉车行驶时喷出的水能浇灌到整个绿化带，请直接写出h的最小值．

查看试题解析
14. 如图1，已知在平面直角坐标系xOy中，四边形OABC是边长为3的正方形，其中顶点A，C分别在x轴的正半轴和y轴的正半轴上．抛物线y=-x²+bx+c经过A，C两点，与x轴交于另一个点D．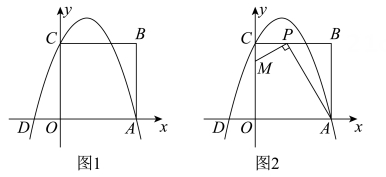

(1)、①求点A，B，C的坐标；
②求b，c的值．

(2)、若点P是边BC上的一个动点，连结AP，过点P作PM⊥AP，交y轴于点M（如图2所示）．当点P在BC上运动时，点M也随之运动．设BP=m，CM=n，试用含m的代数式表示n，并求出n的最大值．

查看试题解析

15. “八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：

①统计售价与需求量的数据，通过描点(图1)，发现该蔬菜需求量y_需求(吨)关于售价x(元/千克)的函数图象可以看成抛物线，其表达式为 $y_{需求} = a x^{2} + c$ ，部分对应值如下表：

售价x(元/千克)	…	2.5	3	3.5	4	…
需求量y_需求(吨）	…	7.75	7.2	6.55	5.8	…

②该蔬菜供给量y_供给(吨)关于售价x(元/千克)的函数表达式为y_供给=x-1，函数图象见图1.

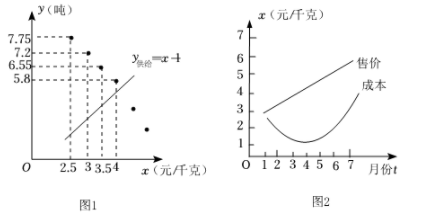
③1~7月份该蔬菜售价x_售价(元/千克)、成本x_成本(元/千克)关于月份t的函数表达式分别为 $x_{售价} = \frac{1}{2} t + 2$ ， $x_{成本} = \frac{1}{4} t^{2} - \frac{3}{2} t + 3$ ，函数图象见图2.

请解答下列问题：

(1)、求a，c的值.

(2)、根据图2，哪个月出售这种蔬菜每千克获利最大？并说明理由.

(3)、求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润.

查看试题解析