浙江省2022年中考数学真题分类汇编04 一次函数与反比例函
试卷更新日期:2022-07-03 类型:二轮复习
一、单选题
-
1. 如图是城市某区域的示意图,建立平面直角坐标系后,学校和体育场的坐标分别是(3,1),(4,-2),下列各地点中,离原点最近的是( )
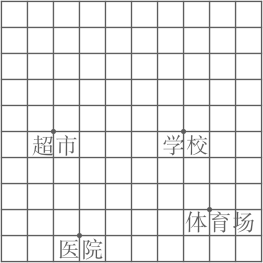 A、超市 B、医院 C、体育场 D、学校2. 吴老师家、公园、学校依次在同一条直线上,家到公园、公园到学校的距离分别为 400m, 600m.他从家出发匀速步行8min到公园后,停留 4min,然后匀速步行6min到学校,设吴老师离公园的距离为y(单位: m),所用时间为x (单位: min),则下列表示y与 x之间函数关系的图象中,正确的是( )A、
A、超市 B、医院 C、体育场 D、学校2. 吴老师家、公园、学校依次在同一条直线上,家到公园、公园到学校的距离分别为 400m, 600m.他从家出发匀速步行8min到公园后,停留 4min,然后匀速步行6min到学校,设吴老师离公园的距离为y(单位: m),所用时间为x (单位: min),则下列表示y与 x之间函数关系的图象中,正确的是( )A、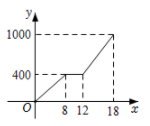 B、
B、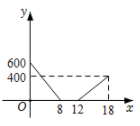 C、
C、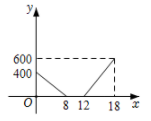 D、
D、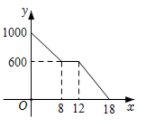 3. 如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1( ,0),M2( ,-1),M3(1,4),M4(2, )四个点中,直线PB经过的点是( )
3. 如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1( ,0),M2( ,-1),M3(1,4),M4(2, )四个点中,直线PB经过的点是( ) A、M1 B、M2 C、M3 D、M44. 小聪某次从家出发去公园游玩的行程如图所示,他离家的路程为s米,所经过的时间为t分钟,下列选项中的图象,能近似刻画s与t之间关系的是( )
A、M1 B、M2 C、M3 D、M44. 小聪某次从家出发去公园游玩的行程如图所示,他离家的路程为s米,所经过的时间为t分钟,下列选项中的图象,能近似刻画s与t之间关系的是( )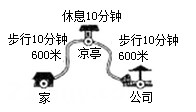 A、
A、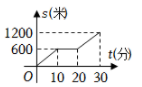 B、
B、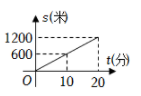 C、
C、 D、
D、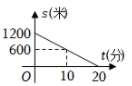 5. 已知 (x1 , x2),(x2 , y2),(x3 , y3)为直线 y=-2x+3 上的三个点,且x1< x2< x3 , 则以下判断正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 已知点A(a,b),B(4,c)在直线y=kx+3(k为常数,k≠0)上,若ab的最大值为9,则c的值为( )A、1 B、 C、2 D、
5. 已知 (x1 , x2),(x2 , y2),(x3 , y3)为直线 y=-2x+3 上的三个点,且x1< x2< x3 , 则以下判断正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 已知点A(a,b),B(4,c)在直线y=kx+3(k为常数,k≠0)上,若ab的最大值为9,则c的值为( )A、1 B、 C、2 D、二、填空题
-
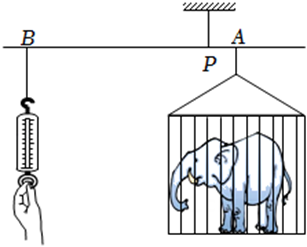
7. 某动物园利用杠杆原理称象;如图,在点P处挂一根质地均匀且足够长的钢梁(呈水平状态),将装有大象的铁笼和弹簧秤(秤的重力忽略不许)分别悬挂在钢梁的点A、B处,当钢梁保持水平时,弹簧秤读数为k(N),若铁笼固定不动,移动弹簧秤使BP扩大到原来的n(n>1)倍,且钢梁保持水平,则弹簧秤读数为(N)(用含n,k的代数式表示)
 8. 已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组 的解是9. 如图,在平面直角坐标系xOy中,点 A (0,4), B(3,4),将△ABO向右平移到 △CDE 位置, A 的对应点是 C, O的对应点是 E,函数 的图象经过点 C 和DE的中点 F,则k的值是 .
8. 已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组 的解是9. 如图,在平面直角坐标系xOy中,点 A (0,4), B(3,4),将△ABO向右平移到 △CDE 位置, A 的对应点是 C, O的对应点是 E,函数 的图象经过点 C 和DE的中点 F,则k的值是 . 10. 如图,在直角坐标系中,△ABC的顶点C与原点O重合,点A在反比例函数y= (k>0,x>0)的图象上,点B的坐标为(4,3),AB与y轴平行,若AB=BC,则k= .
10. 如图,在直角坐标系中,△ABC的顶点C与原点O重合,点A在反比例函数y= (k>0,x>0)的图象上,点B的坐标为(4,3),AB与y轴平行,若AB=BC,则k= . 11. 三个能够重合的正六边形的位置如图.已知B点的坐标是(﹣ ,3),则A点的坐标是
11. 三个能够重合的正六边形的位置如图.已知B点的坐标是(﹣ ,3),则A点的坐标是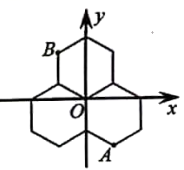 12. 如图,四边形OABC为矩形,点A在第二象限,点A关于OB的对称点为点D,点B,D都在函数y= (x>0)的图象上,BE⊥x轴于点E.若DC的延长线交x轴于点F,当矩形OABC的面积为 时, 的值为 , 点F的坐标为 .
12. 如图,四边形OABC为矩形,点A在第二象限,点A关于OB的对称点为点D,点B,D都在函数y= (x>0)的图象上,BE⊥x轴于点E.若DC的延长线交x轴于点F,当矩形OABC的面积为 时, 的值为 , 点F的坐标为 .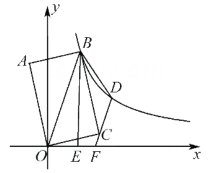 13. 如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是y= ,则图象经过点D的反比例函数的解析式是 .
13. 如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形ABCD.若图象经过点C的反比例函数的解析式是y= ,则图象经过点D的反比例函数的解析式是 .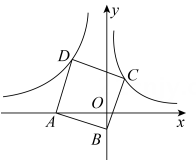
三、综合题
-
14. 如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高 y (单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,当x=6时,y=2.
 (1)、求y关于x的函数解析式;(2)、若火焰的像高为 3cm ,求小孔到蜡烛的距离.15. 如图,正比例函数y= x的图象与反比例函数y= (k≠0)的图象都经过点A(a,2).
(1)、求y关于x的函数解析式;(2)、若火焰的像高为 3cm ,求小孔到蜡烛的距离.15. 如图,正比例函数y= x的图象与反比例函数y= (k≠0)的图象都经过点A(a,2).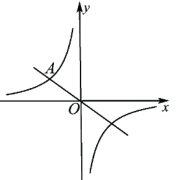 (1)、求点A的坐标和反比例函数表达式.(2)、若点P(m,n)在该反比例函数图象上,且它到y轴距离小于3,请根据图象直接写出n的取值范围.16. 为了落实劳动教育,某学校邀请农科院专家指导学生进行小番茄的种植,经过试验,其平均单株产量y千克与每平方米种植的株数x(2≤x≤8,且x为整数)构成一种函数关系,每平方米种植2株时,平均单株产量为4千克;以同样的栽培条件,每平方米种植的株数每增加1株,单株产量减少0.5千克.(1)、求y关于x的函数表达式.(2)、每平方米种植多少株时,能获得最大的产量?最大产量为多少下克?17. 某校组织学生从学校出发,乘坐大巴前往基地进行研学活动.大巴出发1小时后,学校因事派人乘坐轿车沿相同路线追赶.已知大巴行驶的速度是40千米/小时,轿车行驶的速度是60千米/小时.
(1)、求点A的坐标和反比例函数表达式.(2)、若点P(m,n)在该反比例函数图象上,且它到y轴距离小于3,请根据图象直接写出n的取值范围.16. 为了落实劳动教育,某学校邀请农科院专家指导学生进行小番茄的种植,经过试验,其平均单株产量y千克与每平方米种植的株数x(2≤x≤8,且x为整数)构成一种函数关系,每平方米种植2株时,平均单株产量为4千克;以同样的栽培条件,每平方米种植的株数每增加1株,单株产量减少0.5千克.(1)、求y关于x的函数表达式.(2)、每平方米种植多少株时,能获得最大的产量?最大产量为多少下克?17. 某校组织学生从学校出发,乘坐大巴前往基地进行研学活动.大巴出发1小时后,学校因事派人乘坐轿车沿相同路线追赶.已知大巴行驶的速度是40千米/小时,轿车行驶的速度是60千米/小时.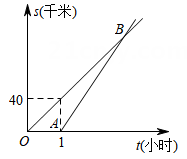 (1)、求轿车出发后多少小时追上大巴?此时,两车与学校相距多少千米?(2)、如图,图中OB,AB分别表示大巴、轿车离开学校的路程s(千米)与大巴行驶的时间t(小时)的函数关系的图象.试求点B的坐标和AB所在直线的解析式;(3)、假设大巴出发a小时后轿车出发追赶,轿车行驶了1.5小时追上大巴,求a的值.18. 设函数y1= ,函数y2=k2x+b(k1 , k2 , b是常数,k1≠0,k2≠0).(1)、若函数y1和函数y2的图象交于点A(1,m),点B(3,1),
(1)、求轿车出发后多少小时追上大巴?此时,两车与学校相距多少千米?(2)、如图,图中OB,AB分别表示大巴、轿车离开学校的路程s(千米)与大巴行驶的时间t(小时)的函数关系的图象.试求点B的坐标和AB所在直线的解析式;(3)、假设大巴出发a小时后轿车出发追赶,轿车行驶了1.5小时追上大巴,求a的值.18. 设函数y1= ,函数y2=k2x+b(k1 , k2 , b是常数,k1≠0,k2≠0).(1)、若函数y1和函数y2的图象交于点A(1,m),点B(3,1),①求函数y1 , y2的表达式:
②当2<x<3时,比较y1与y2的大小(直接写出结果).
(2)、若点C(2,n)在函数y1的图象上,点C先向下平移2个单位,再向左平移4个单位,得点D,点D恰好落在函数y1的图象上,求n的值,19. 已知反比例函数 的图象的一支如图所示,它经过点 (3,-2). (1)、求这个反比例函数的表达式,并补画该函数图象的另一支.(2)、求当 y≤5,且y≠0时自变量x的取值范围.20. 一个深为6米的水池积存着少量水,现在打开水阀进水,下表记录了2小时内5个时刻的水位高度,其中x表示进水用时(单位:小时),y表示水位高度(单位:米).
(1)、求这个反比例函数的表达式,并补画该函数图象的另一支.(2)、求当 y≤5,且y≠0时自变量x的取值范围.20. 一个深为6米的水池积存着少量水,现在打开水阀进水,下表记录了2小时内5个时刻的水位高度,其中x表示进水用时(单位:小时),y表示水位高度(单位:米).x
0
0.5
1
1.5
2
y
1
1.5
2
2.5
3
为了描述水池水位高度与进水用时的关系,现有以下三种函数模型供选择: ( ),y=ax2+bx+c ( ), ( ).
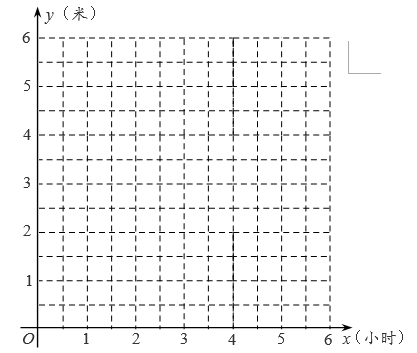 (1)、在平面直角坐标系中描出表中数据对应的点,再选出最符合实际的函数模型,求出相应的函数表达式,并画出这个函数的图象.(2)、当水位高度达到5米时,求进水用时x.21. 如图,点A在第一象限内,AB⊥x轴于点B,反比例函数 的图象分别交AO,AB于点C,D.已知点C的坐标为(2,2),BD=1.
(1)、在平面直角坐标系中描出表中数据对应的点,再选出最符合实际的函数模型,求出相应的函数表达式,并画出这个函数的图象.(2)、当水位高度达到5米时,求进水用时x.21. 如图,点A在第一象限内,AB⊥x轴于点B,反比例函数 的图象分别交AO,AB于点C,D.已知点C的坐标为(2,2),BD=1. (1)、求k的值及点D的坐标.(2)、已知点P在该反比例函数图象上,且在△ABO的内部(包括边界),直接写出点P的横坐标x的取值范围.22. 因疫情防控需要,一辆货车先从甲地出发运送防疫物资到乙地,稍后一辆轿车从甲地急送防疫专家到乙地.已知甲、乙两地的路程是330km,货车行驶时的速度是60km/h.两车离甲地的路程s(km)与时间t(h)的函数图象如图.
(1)、求k的值及点D的坐标.(2)、已知点P在该反比例函数图象上,且在△ABO的内部(包括边界),直接写出点P的横坐标x的取值范围.22. 因疫情防控需要,一辆货车先从甲地出发运送防疫物资到乙地,稍后一辆轿车从甲地急送防疫专家到乙地.已知甲、乙两地的路程是330km,货车行驶时的速度是60km/h.两车离甲地的路程s(km)与时间t(h)的函数图象如图.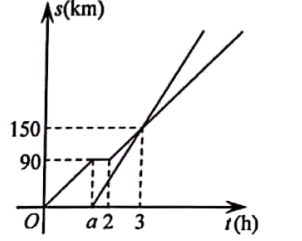 (1)、求出a的值;(2)、求轿车离甲地的路程s(km)与时间t(h)的函数表达式:(3)、问轿车比货车早多少时间到达乙地?23. 6月13日,某港口的湖水高度y(cm)和时间x(h)的部分数据及函数图象如下:
(1)、求出a的值;(2)、求轿车离甲地的路程s(km)与时间t(h)的函数表达式:(3)、问轿车比货车早多少时间到达乙地?23. 6月13日,某港口的湖水高度y(cm)和时间x(h)的部分数据及函数图象如下:x(b)
……
11
12
13
14
15
16
17
18
……
y(cm)
……
189
137
103
80
101
133
202
260
……
(数据来自某海举研究所)
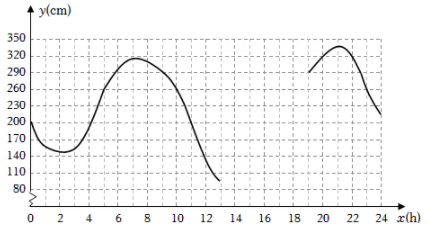 (1)、数学活动:
(1)、数学活动:①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当x=4时,y的值为多少?当y的值最大时,x的值为多少?
(2)、数学思考:请结合函数图象,写出该函数的两条性质或结论.
(3)、数学应用:根据研究,当潮水高度超过260cm时,货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?