山东省威海市2022年中考数学真题
试卷更新日期:2022-07-01 类型:中考真卷
一、单选题
-
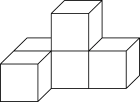
1. -5的相反数是( )A、 B、 C、5 D、-52. 如图所示的几何体是由五个大小相同的小正方体搭成的.其俯视图是( )
 A、
A、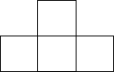 B、
B、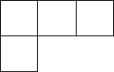 C、
C、 D、
D、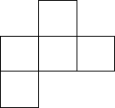 3. 一个不透明的袋子中装有2个红球、3个白球和4个黄球,每个球除颜色外都相同.从中任意摸出1个球,摸到红球的概率是( )A、 B、 C、 D、4. 下列计算正确的是( )A、a3•a3=a9 B、(a3)3=a6 C、a6÷a3=a2 D、a3+a3=2a35. 图1是光的反射规律示意图.其中,PO是入射光线,OQ是反射光线,法线KO⊥MN,∠POK是入射角,∠KOQ是反射角,∠KOQ=∠POK.图2中,光线自点P射入,经镜面EF反射后经过的点是( )
3. 一个不透明的袋子中装有2个红球、3个白球和4个黄球,每个球除颜色外都相同.从中任意摸出1个球,摸到红球的概率是( )A、 B、 C、 D、4. 下列计算正确的是( )A、a3•a3=a9 B、(a3)3=a6 C、a6÷a3=a2 D、a3+a3=2a35. 图1是光的反射规律示意图.其中,PO是入射光线,OQ是反射光线,法线KO⊥MN,∠POK是入射角,∠KOQ是反射角,∠KOQ=∠POK.图2中,光线自点P射入,经镜面EF反射后经过的点是( ) A、A点 B、B点 C、C点 D、D点6. 如图,在方格纸中,点P,Q,M的坐标分别记为(0,2),(3,0),(1,4).若MN∥PQ,则点N的坐标可能是( )
A、A点 B、B点 C、C点 D、D点6. 如图,在方格纸中,点P,Q,M的坐标分别记为(0,2),(3,0),(1,4).若MN∥PQ,则点N的坐标可能是( )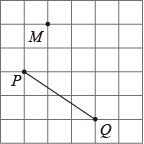 A、(2,3) B、(3,3) C、(4,2) D、(5,1)7. 试卷上一个正确的式子()÷★=被小颖同学不小心滴上墨汁.被墨汁遮住部分的代数式为( )A、 B、 C、 D、8. 如图,二次函数y=ax2+bx(a≠0)的图像过点(2,0),下列结论错误的是( )
A、(2,3) B、(3,3) C、(4,2) D、(5,1)7. 试卷上一个正确的式子()÷★=被小颖同学不小心滴上墨汁.被墨汁遮住部分的代数式为( )A、 B、 C、 D、8. 如图,二次函数y=ax2+bx(a≠0)的图像过点(2,0),下列结论错误的是( )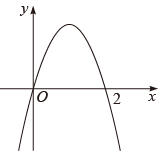 A、b>0 B、a+b>0 C、x=2是关于x的方程ax2+bx=0(a≠0)的一个根 D、点(x1 , y1),(x2 , y2)在二次函数的图象上,当x1>x2>2时,y2<y1<09. 过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是( )A、
A、b>0 B、a+b>0 C、x=2是关于x的方程ax2+bx=0(a≠0)的一个根 D、点(x1 , y1),(x2 , y2)在二次函数的图象上,当x1>x2>2时,y2<y1<09. 过直线l外一点P作直线l的垂线PQ.下列尺规作图错误的是( )A、 B、
B、 C、
C、 D、
D、 10. 由12个有公共顶点O的直角三角形拼成如图所示的图形,∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB位似的三角形的面积为( )
10. 由12个有公共顶点O的直角三角形拼成如图所示的图形,∠AOB=∠BOC=∠COD=…=∠LOM=30°.若S△AOB=1,则图中与△AOB位似的三角形的面积为( )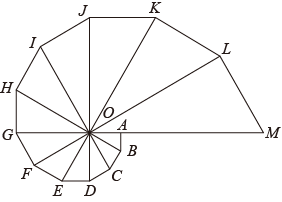 A、()3 B、()7 C、()6 D、()6
A、()3 B、()7 C、()6 D、()6二、填空题
-
11. 因式分解= .12. 若关于x的一元二次方程有两个不相等的实数根,则m的取值范围是 .13. 某小组6名学生的平均身高为acm,规定超过acm的部分记为正数,不足acm的部分记为负数,他们的身高与平均身高的差值情况记录如下表:
学生序号
1
2
3
4
5
6
身高差值(cm)
+2
x
+3
﹣1
﹣4
﹣1
据此判断,2号学生的身高为 cm.
14. 按照如图所示的程序计算,若输出y的值是2,则输入x的值是 .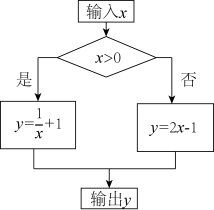 15. 正方形ABCD在平面直角坐标系中的位置如图所示,点A的坐标为(2,0),点B的坐标为(0,4).若反比例函数y=(k≠0)的图象经过点C,则k的值为 .
15. 正方形ABCD在平面直角坐标系中的位置如图所示,点A的坐标为(2,0),点B的坐标为(0,4).若反比例函数y=(k≠0)的图象经过点C,则k的值为 . 16. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则mn= .
16. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则mn= .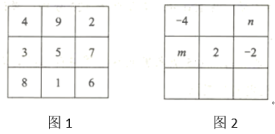
三、解答题
-
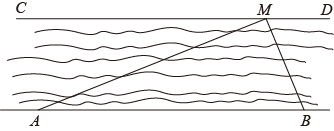
17. 解不等式组,并把解集在数轴上表示出来: .18. 小军同学想利用所学的“锐角三角函数”知识测量一段两岸平行的河流宽度.他先在河岸设立A,B两个观测点,然后选定对岸河边的一棵树记为点M.测得AB=50m,∠MAB=22°,∠MBA=67°.请你依据所测数据求出这段河流的宽度(结果精确到0.1m).
参考数据:sin22°≈ , cos22°≈ , tan22°≈ , sin67°≈ , cos67°≈ , tan67°≈ .
 19. 某学校开展“家国情•诵经典”读书活动.为了解学生的参与程度,从全校学生中随机抽取200人进行问卷调查,获取了他们每人平均每天阅读时间的数据(m/分钟).将收集的数据分为A,B,C,D,E五个等级,绘制成如下统计图表(尚不完整):
19. 某学校开展“家国情•诵经典”读书活动.为了解学生的参与程度,从全校学生中随机抽取200人进行问卷调查,获取了他们每人平均每天阅读时间的数据(m/分钟).将收集的数据分为A,B,C,D,E五个等级,绘制成如下统计图表(尚不完整):平均每天阅读时间统计表
等级
人数(频数)
A(10≤m<20)
5
B(20≤m<30)
10
C(30≤m<40)
x
D(40≤m<50)
80
E(50≤m≤60)
y

请根据图表中的信息,解答下列问题:
(1)、求x的值;(2)、这组数据的中位数所在的等级是;(3)、学校拟将平均每天阅读时间不低于50分钟的学生评为“阅读达人”予以表扬.若全校学生以1800人计算,估计受表扬的学生人数.20. 如图,四边形ABCD是⊙O的内接四边形,连接AC,BD,延长CD至点E.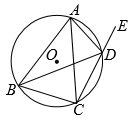 (1)、若AB=AC,求证:∠ADB=∠ADE;(2)、若BC=3,⊙O的半径为2,求sin∠BAC.21. 某农场要建一个矩形养鸡场,鸡场的一边靠墙,另外三边用木栅栏围成.已知墙长25m,木栅栏长47m,在与墙垂直的一边留出1m宽的出入口(另选材料建出入门).求鸡场面积的最大值.
(1)、若AB=AC,求证:∠ADB=∠ADE;(2)、若BC=3,⊙O的半径为2,求sin∠BAC.21. 某农场要建一个矩形养鸡场,鸡场的一边靠墙,另外三边用木栅栏围成.已知墙长25m,木栅栏长47m,在与墙垂直的一边留出1m宽的出入口(另选材料建出入门).求鸡场面积的最大值.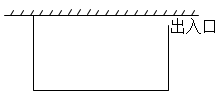 22. 如图:
22. 如图: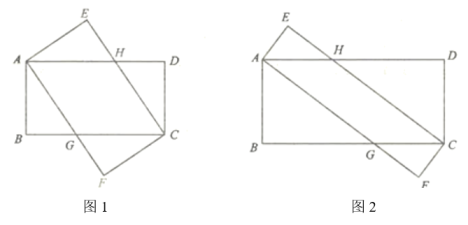 (1)、将两张长为8,宽为4的矩形纸片如图1叠放.
(1)、将两张长为8,宽为4的矩形纸片如图1叠放.①判断四边形AGCH的形状,并说明理由;
②求四边形AGCH的面积.
(2)、如图2,在矩形ABCD和矩形AFCE中,AB=2 , BC=7,CF= , 求四边形AGCH的面积.23. 探索发现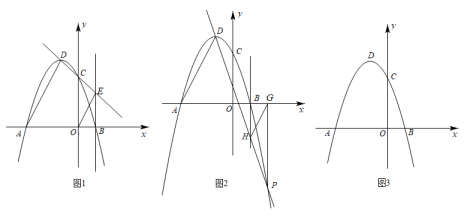 (1)、在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D,连接AD.
(1)、在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D,连接AD.①如图1,直线DC交直线x=1于点E,连接OE.求证:AD∥OE;
②如图2,点P(2,﹣5)为抛物线y=ax2+bx+3(a≠0)上一点,过点P作PG⊥x轴,垂足为点G.直线DP交直线x=1于点H,连接HG.求证:AD∥HG;
(2)、通过上述两种特殊情况的证明,你是否有所发现?请仿照(1)写出你的猜想,并在图3上画出草图.在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣3,0),B(1,0),顶点为点D.点M为该抛物线上一动点(不与点A,B,D重合),猜想:作MN⊥x轴于N,直线DM交直线x=1于Q,则QN∥AD,证明见解析
24. 回顾:用数学的思维思考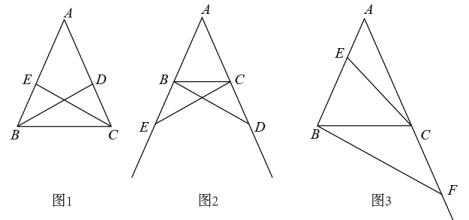 (1)、如图1,在△ABC中,AB=AC.
(1)、如图1,在△ABC中,AB=AC.①BD,CE是△ABC的角平分线.求证:BD=CE.
②点D,E分别是边AC,AB的中点,连接BD,CE.求证:BD=CE.
(从①②两题中选择一题加以证明)
(2)、猜想:用数学的眼光观察经过做题反思,小明同学认为:在△ABC中,AB=AC,D为边AC上一动点(不与点A,C重合).对于点D在边AC上的任意位置,在另一边AB上总能找到一个与其对应的点E,使得BD=CE.进而提出问题:若点D,E分别运动到边AC,AB的延长线上,BD与CE还相等吗?请解决下面的问题:
如图2,在△ABC中,AB=AC,点D,E分别在边AC,AB的延长线上,请添加一个条件(不再添加新的字母),使得BD=CE,并证明.
(3)、探究:用数学的语言表达如图3,在△ABC中,AB=AC=2,∠A=36°,E为边AB上任意一点(不与点A,B重合),F为边AC延长线上一点.判断BF与CE能否相等.若能,求CF的取值范围;若不能,说明理由.