河南省信阳市浉河区2021-2022学年七年级下学期期末数学试卷
试卷更新日期：2022-07-01 类型：期末考试
一、选择题（每小题3分，共30分）
-
1. 近段时间，以熊猫为原型的2022北京冬奥会吉祥物“冰墩墩”成了全网“顶流”．如图，通过平移图吉祥物“冰墩墩”可以得到的图形是（ ）
A、
B、
C、
D、
2. 下列调查中，适合于采用普查方式的是（ ）A、调查央视“五一晚会”的收视率 B、了解信阳市民对南湾湖旅游景点的印象 C、了解一批新型节能灯的使用寿命 D、了解某航班上的乘客是否都持有“绿色健康码”3. 下列实数中，无理数是（ ）A、3.1415926 B、﹣0.2022 C、 D、4. 如图摆放着一副三角尺，∠B＝∠EDF＝90°，点E在AC上，点D在BC的延长线上，EF∥BC，∠A＝30°，∠F＝45°，则∠CED的度数为（ ）
A、15° B、20° C、30° D、45°5. 在平面直角坐标系中，点P（﹣2021，2022）在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 方程组 的解为 ，则被遮盖的前后两个数分别为（ ）A、1、2 B、1、5 C、5、1 D、2、47. 不等式组 的解集在数轴上表示为（ ）A、
B、
C、
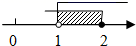D、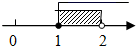
8. 如图，在平面直角坐标系中，点A、B的坐标分别为（2，0），（0，1），将线段AB平移至A'B'，那么a+b的值为（ ）
A、2 B、3 C、4 D、59. 下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容，则回答正确的是（ ）已知：如图，∠BEC＝∠B+∠C，求证：AB∥CD．
证明：延长BE交（※）于点F，则∠BEC＝（⊙）+∠C．
又∵∠BEC＝∠B+∠C，
∴∠B＝（▲）
∴AB∥CD（（□）相等，两直线平行）
A、⊙代表∠FEC B、□代表同位角 C、▲代表∠EFC D、※代表AB10. 如图，在平面直角坐标系中，AB∥EG∥x轴，BC∥DE∥HG∥AP∥y轴，点D、C、P、H在x轴上，A（1，2），B（﹣1，2），D（﹣3，0），E（﹣3，﹣2），G（3，﹣2），把一条长为2022个单位长度且没有弹性的细线（细线的粗细忽略不计）的一端固定在点A处，并按A→B→C→D→E→F→G→H→P→A…的规律紧绕在图形“凸”的边上，则细线另一端所在位置的点的坐标是（ ）
A、（﹣1，2） B、（﹣1，1） C、（0，1） D、（0，2）二、填空题（每小题3分，共15分）
-
11. 写出一个比 小的无理数 ．12. 方程组 的解为 ．13. 5﹣ 的整数部分是 ．14. “今有四十鹿进舍，小舍容四鹿，大舍容六鹿，需舍几何？（改编自《缉古算经》）”大意为．今有50只鹿进圈舍，小圈舍可以容纳4头鹿，大圈舍可以容纳6头鹿，且恰好每个圈舍都能放满，求所需圈舍的间数．设所需大圈舍x间，小圈舍y间，则x+y求得的结果有 种．15. 在数学著作《算术研究》一书中，对于任意实数，通常用[x]表示不超过x的最大整数，如：[π]＝3，[2]＝2，[﹣2.1]＝﹣3．当﹣1＜x＜1时，[1+x]+[1﹣x]的值为 ．
三、解答题（本大题共8个小题，满分75分）
-
16.(1)、计算：﹣12022+ ﹣ ；(2)、解方程组： ．17. 解不等式组 ，并求它的所有的非负整数解．18. 农业科技兴趣小组为了解西红柿挂果情况从丰收一号蔬菜大棚中随机收集到50株西红柿秧上小西红柿的个数：
28 62 54 29 32 47 68 37 55 43 35 50 46 54 39 57 51 54 52 59 38 51 47 39 64 61 59 48 56 45 53 49 36 64 39 52 63 65 48 58 59 64 45 54 48 40 42 46 60 62
个数x
频数
百分比
25≤x＜35
3
6%
35≤x＜45
10
20%
45≤x＜55
20
a
55≤x＜65
b
c
65≤x＜75
2
4%
合计
50
100%
(1)、a＝ ， b＝ ， c＝ ， 并补全频数分布直方图；(2)、若丰收一号蔬菜大棚中共有西红柿秧500株，估计挂果个数在35≤x＜55之间的西红柿秧的株数．19. 如图，四边形ABCD，四个顶点分别是A（﹣2，﹣1），B（1，﹣3），C（4，﹣1），D（1，1）．将四边形ABCD向上平移3个单位长度，再向左平移2个单位长度得到四边形A1B1C1D1 ．
(1)、画出四边形A1B1C1D1 ， 并直接写出A1、C1两点的坐标；(2)、求出四边形A1B1C1D1的面积．20. 2022年北京冬奥会、冬残奥会已圆满结束，活泼敦厚的“冰墩墩”，喜庆祥和的“雪容融”引起广大民众的喜爱．王老师想要购买这两种吉祥物作为本次冬奥会的纪念品，已知购买2件“冰墩墩”和1件“雪容融”共需150元，购买3件“冰墩墩”和2件“雪容融”共需245元．
(1)、求“冰墩墩”和“雪容融”的单价；(2)、学校现需一次性购买上述型号的“冰墩墩”和“雪容融”纪念品共100个，要求购买的总费用不超过5000元，则最多可以购买多少个“冰墩墩”？21. 在平面直角坐标系中，点P（a，b），Q（c，d）给出如下定义：对于实数k（k≠0），我们称点M（ka+kc，kb+kd）为P，Q两点的“k”系和点．例如，点P（3，4），Q（1，﹣2），则点P，Q的“ ”系和点的坐标为：（2，1），如图，已知点A（4，﹣1），B（﹣2，﹣1）．
(1)、直接写出点A，B的“2”系和点坐标为 ；(2)、若点A为B，C的“﹣3”系和点求点C的坐标；(3)、若点D为A，B的“k”系和点，三角形ABD的面积为6，则符合条件的k的值为 ．22. 如图1，AB、BC被直线AC所截，点D是线段AC上的点，过点D作DE∥AB，连接AE，∠B＝∠E＝75°．
(1)、求证：AE∥BC；(2)、将线段AE沿着直线AC平移得到线段PQ，连接DQ．如图2，当DE⊥DQ时，求∠Q的度数．23. 如图，在平面直角坐标系中，点A、B的坐标分别为A（0，a），B（b，0），且a、b满足|2a﹣b﹣6|+ ＝0，点C在x轴的负半轴上，连接AB、AC．
(1)、如图1，若△AOC的面积是△AOB面积的 倍，求点C的坐标；(2)、如图2，在（1）的条件下，点P从点O出发以每秒1个单位长度的速度沿OB方向移动，同时点Q从点A出发以每秒2个单位长度的速度在AO间往返移动，即先沿AO方向移动，到达点O反向移动．设移动的时间为t秒，四边形ACQB与△ABP的面积分别记为S1、S2 ， 若存在时间t（0≤t≤5）使S1＝4S2 ， 直接写出t值 .