浙江省余姚市2021-2022学年八年级下学期数学期末考试试卷

试卷更新日期：2022-07-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个图标中，属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式计算正确的是（）

A、 $8 \sqrt{3} - 2 \sqrt{3} = 6$ B、 $5 \sqrt{3} + 5 \sqrt{2} = 10 \sqrt{5}$ C、 $4 \sqrt{3} \times 2 \sqrt{2} = 8 \sqrt{6}$ D、 $4 \sqrt{2} \div 2 \sqrt{2} = 2 \sqrt{2}$

查看试题解析
3. 二次根式 $\sqrt{x - 5}$ 中字母x的取值可以是（）

A、x＝5 B、x＝1 C、x＝2 D、x＝-1

查看试题解析
4. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数都是8环，方差分别是 $S_{甲}^{2} = 0.61$ ， $S_{乙}^{2} = 0.52$ ， $S_{丙}^{2} = 0.53$ ， $S_{丁}^{2} = 0.42$ ，则射击成绩比较稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 若关于 x 的方程 $x^{2} + a x + a = 0$ 有一个根为﹣3，则a的值是（）

A、9 B、4.5 C、3 D、﹣3

查看试题解析
6. 若反比例函数 $y = \frac{k}{x}$ 的图像经过 $(2 ， - 1)$ ，则k的值是（）

A、2 B、 $\frac{1}{2}$ C、-2 D、 $- \frac{1}{2}$

查看试题解析
7. 某校为落实“光盘行动”，对每天的剩饭菜进行称重，第一周的剩余量为20kg，第三周为9.8kg，设每周剩余量的平均减少率为x，则可列方程（）

A、20（1﹣x）²＝9.8 B、20（1+x）²＝9.8 C、20（1﹣2x）＝9.8 D、20（1+2x）＝9.8

查看试题解析
8. 用如下算式计算方差： $S^{2} = \frac{1}{n} [{(x_{1} - 2)}^{2} + {(x_{2} - 2)}^{2} + {(x_{3} - 2)}^{2} + \dots + {(x_{n} - 2)}^{2}]$ ，上述算式中的“ 2 ”是这组数据的（）

A、最小值 B、平均数 C、中位数 D、众数

查看试题解析
9. 如图，在△ABC中，∠C＝50°，AC＝BC，点D在AC边上，以AB，AD为边作▱ABED，则∠E的度数为（）

A、50° B、55° C、65° D、70°

查看试题解析
10. 如图，台阶阶梯每一层高20cm，宽30cm，长50cm，一只蚂蚁从A点爬到B点，最短路程是（）

A、 $10 \sqrt{89}$ B、 $50 \sqrt{5}$ C、120 D、130

查看试题解析

二、填空题(每题4分，共24分)

11. 若二次根式 $\sqrt{x - 3}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 用反证法证明“在三角形中至少有一个内角大于或等于60°”，应先假设命题不成立，即三角形的三个内角都60°（填“＞”“＜”或“＝”）.

查看试题解析
13. 某校规定：学生的单科学期综合成绩是由平时、期中和期末三项成绩按3∶3∶4的比例计算所得．已知某学生本学期数学的平时、期中和期末成绩分别是80分、90分和85分，那么他本学期数学学期综合成绩是分。

查看试题解析
14. 一元二次方程x²+bx+2021＝0的一个根为x＝﹣1，则b的值为.

查看试题解析
15. 如图，AB∥CD，AB＝CD，若点E在直线CD上，△ABE的面积为30，则四边形ABCD的面积.

查看试题解析
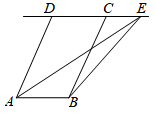16. 如图，四边形ABCD中，AD∥BC，且∠B＋∠C＝90°，分别以AB、AD、DC为边向形外作正方形ABEF、正方形ADHG、正方形DCJI，且其面积依次记为S₁、S₂、S₃ ，若S₁＋S₃＝4S₂ ，则 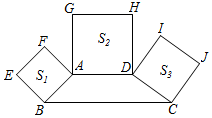$\frac{B C}{A D}$ ＝．

查看试题解析

三、解答题(共7小题，满分66分)

17.

(1)、 $\sqrt{12} + \sqrt{5} \times \sqrt{15}$ ；

(2)、 ${(\sqrt{2} - \sqrt{3})}^{2} + \sqrt{24}$ ．

查看试题解析
18. 求证：在直角坐标系中，点A(x，y)与点B(-x，-y)关于原点成中心对称.

查看试题解析
19. 某公司计划从两家皮具生产能力相近的制造厂选择一家来承担外销业务，这两家厂生产的皮具款式和材料都符合要求，因此只需要检测皮具质量的克数是否稳定．现从两家提供的样品中各抽查10件，测得它们的质量如下（单位：克）
甲：500，499，500，500，503，498，497，502，500，501，
乙：499，500，498，501，500，501，500，499，500，502

(1)、【甲】平均数：方差：
【乙】平均数：方差：

(2)、你认为该选择哪一家制造厂，请说明理由。

查看试题解析
20. 如图，在▱ABCD中，E，F分别是BC，AD的中点，连结AE，CF.求证：AE＝CF.

查看试题解析
21. 如图，平行四边形ABCD放置在平面直角坐标系中，已知点A（﹣2，0），B（﹣6，0），D（0，3），点C在反比例函数y $= \frac{k}{x}$ 的图象上.

(1)、直接写出点C坐标，并求反比例函数的表达式；

(2)、将平行四边形ABCD向上平移得到平行四边形EFGH，使点F在反比例函数y $= \frac{k}{x}$ 的图象上，GH与反比例函数图象交于点M.连结AE，求AE的长及点M的坐标.

查看试题解析
22. 如图，在四边形ABCD中，AC、BD相交于点O，O是AC的中点，AB//DC，AC=20，BD=10．

(1)、求证：四边形ABCD是平行四边形；

(2)、若AC⊥BD，求平行四边形ABCD的面积．

查看试题解析
23. △ABC是一块腰长为20cm的等腰直角三角形白铁皮零料．请你利用三角形零料裁出一块矩形白铁皮，并使矩形的四个顶点都在三角形的边上．
活动一：若裁出的矩形白铁皮的面积为零料面积的 $\frac{3}{8}$ ，请画出符合题意的裁剪示意图（一种即可），并求出此时矩形铁皮的边长．

活动二：根据“活动一”中你选择的裁剪方法，思考并解答：

①是否能够使得裁出的矩形白铁皮的面积是零料面积的 $\frac{3}{4}$ ？请判断并说明理由；

②猜想裁剪出的矩形白铁皮的面积最大值．直接写出结论，不必说理．

查看试题解析
24. 在正方形ABCD中，连结BD，O为BD中点，点E在线段OD上（不与点O，D重合）.

(1)、如图1，过点E作EF⊥AB于点F，EG⊥BC于点G.分别判断EF与EG的数量与位置关系，并说明理由.

(2)、如图2，连结EC，过点E作EH⊥EC，交AB于点H.
①求证：EH＝EC.
②猜想OE与BH的数量关系，并证明.

查看试题解析