浙江省丽水市2021-2022学年高一下学期数学普通高中教学质量监控(期末)试卷
试卷更新日期:2022-07-01 类型:期末考试
一、单选题
-
1. 若复数满足(为虚数单位),则等于( )A、 B、 C、 D、2. 若为非零向量,则“”是“共线”的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件3. 从某中学抽取名同学,他们的数学成绩如下:82,85,88,90,92,92,92,96,96,98(单位:分),则这10名同学数学成绩的众数,第75百分位数分别为( )A、92,85 B、92,88 C、92,96 D、96,964. 若 ,则事件 与 的关系是( )A、事件 与 互斥 B、事件 与 对立 C、事件 与 相互独立 D、事件 与 既互斥又相互独立5. 某校高一年级1000名学生的血型统计情况如图所示.某课外兴趣小组为了研究血型与饮食之间的关系,决定采用分层随机抽样的方法从中抽取一个容量为100的样本,则从高一年级A型血的学生中应抽取的人数是( )
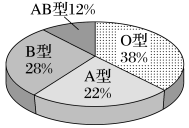 A、11 B、22 C、110 D、2206. 为了得到函数的图象,只要把的图象( )A、向右平移个单位长度,然后纵坐标不变,横坐标伸长为原来的3倍 B、向左平移个单位长度,然后纵坐标不变,横坐标缩短为原来的倍 C、纵坐标不变,横坐标缩短为原来的倍,再向右平移个单位长度 D、纵坐标不变,横坐标缩短为原来的倍,再向右平移个单位长度7. 《九章算术》是我国古代的数学巨著,其卷第五“商功”有如下的问题:“今有刍甍,下广三丈,袤六丈,上袤四丈,无广,高一丈.问积几何?”意思为:今有底面为矩形的屋脊形状的多面体(如图),下底面宽丈,长丈,上棱丈,与平面平行,与平面的距离为丈,则它的体积是( )
A、11 B、22 C、110 D、2206. 为了得到函数的图象,只要把的图象( )A、向右平移个单位长度,然后纵坐标不变,横坐标伸长为原来的3倍 B、向左平移个单位长度,然后纵坐标不变,横坐标缩短为原来的倍 C、纵坐标不变,横坐标缩短为原来的倍,再向右平移个单位长度 D、纵坐标不变,横坐标缩短为原来的倍,再向右平移个单位长度7. 《九章算术》是我国古代的数学巨著,其卷第五“商功”有如下的问题:“今有刍甍,下广三丈,袤六丈,上袤四丈,无广,高一丈.问积几何?”意思为:今有底面为矩形的屋脊形状的多面体(如图),下底面宽丈,长丈,上棱丈,与平面平行,与平面的距离为丈,则它的体积是( ) A、8立方丈 B、6立方丈 C、5立方丈 D、4立方丈8. 如图,直四棱柱的底面是边长为2的正方形, , 分别是的中点,过点的平面记为 , 则下列说法中错误的是( )
A、8立方丈 B、6立方丈 C、5立方丈 D、4立方丈8. 如图,直四棱柱的底面是边长为2的正方形, , 分别是的中点,过点的平面记为 , 则下列说法中错误的是( ) A、点到平面的距离与点到平面α的距离之比为 B、平面截直四棱柱所得截面的面积为 C、平面将直四棱柱分割成的上、下两部分的体积之比为49︰25 D、平面截直四棱柱所得截面的形状为五边形
A、点到平面的距离与点到平面α的距离之比为 B、平面截直四棱柱所得截面的面积为 C、平面将直四棱柱分割成的上、下两部分的体积之比为49︰25 D、平面截直四棱柱所得截面的形状为五边形二、多选题
-
9. 设 为复数, .下列命题中正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则10. 已知 为的三内角的对边,下列命题中正确的是( )A、在中,的充要条件是 B、在锐角中,不等式恒成立 C、在中,若 , 则必是等腰直角三角形 D、在中,若 , , 则必是等边三角形11. 如图,在四边形中, , , , 是边上一点,且 , 是的中点,则下列关系式正确的是( )
 A、 B、 C、 D、12. 如图,在直角梯形中,满足∥ , , 且为正三角形,将沿翻折成三棱锥 , 记与平面所成的角为 , 与平面所成的角为 , 与所成的角为 , 则在翻折过程中,下列结论一定成立的是( )
A、 B、 C、 D、12. 如图,在直角梯形中,满足∥ , , 且为正三角形,将沿翻折成三棱锥 , 记与平面所成的角为 , 与平面所成的角为 , 与所成的角为 , 则在翻折过程中,下列结论一定成立的是( )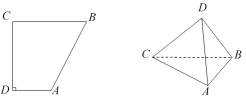 A、 B、 C、 D、
A、 B、 C、 D、三、填空题
-
13. 已知向量 , , 则在上的投影向量为 .14. 有一个多边形水平放置的斜二测直观图是直角梯形(如图所示), , , , 则原多边形面积为 .
 15. 抛掷一枚骰子,记为事件“出现点数是奇数”,为事件“出现点数是3的倍数”,则= .16. 如图,正四面体的棱长为1,点是该正四面体内切球球面上的动点,点是上的动点,则的取值范围为 .
15. 抛掷一枚骰子,记为事件“出现点数是奇数”,为事件“出现点数是3的倍数”,则= .16. 如图,正四面体的棱长为1,点是该正四面体内切球球面上的动点,点是上的动点,则的取值范围为 .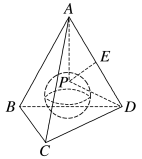 17. 在矩形中, , , , 是平面内的动点,且 , 若 , 则的最小值为 .
17. 在矩形中, , , , 是平面内的动点,且 , 若 , 则的最小值为 .
四、解答题
-
18. 如图,一半径为4米的水轮,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动一圈,如果当水轮上点P从水中浮现时(图中点P0)开始计时,当水轮转动90秒时,点P距离水面米.
 19. 某校为了解学生课外阅读的情况,随机统计了100名学生的一个学期课外阅读时间,所得数据都在中,其频率分布直方图如图所示.
19. 某校为了解学生课外阅读的情况,随机统计了100名学生的一个学期课外阅读时间,所得数据都在中,其频率分布直方图如图所示. (1)、求图中的值以及在中的学生数;(2)、根据频率分布直方图,估计该校学生一个学期课外阅读平均时间.20. 设为的三内角的对边, , .(1)、求的大小;(2)、在下列两个条件中选择一个作为已知,使△ABC存在且唯一确定,并求出BC边上的中线的长度.①周长为;②面积为21. 如图,底面是边长为4的正方形,半圆面底面 . 点为半圆弧(不含 , )上一动点.
(1)、求图中的值以及在中的学生数;(2)、根据频率分布直方图,估计该校学生一个学期课外阅读平均时间.20. 设为的三内角的对边, , .(1)、求的大小;(2)、在下列两个条件中选择一个作为已知,使△ABC存在且唯一确定,并求出BC边上的中线的长度.①周长为;②面积为21. 如图,底面是边长为4的正方形,半圆面底面 . 点为半圆弧(不含 , )上一动点. (1)、求证:;(2)、当点为弧中点时,求二面角的正切值.
(1)、求证:;(2)、当点为弧中点时,求二面角的正切值.
