河南省郑州市巩义、中牟、登封等六县2021-2022学年高一下学期数学期末测评试卷
试卷更新日期:2022-07-01 类型:期末考试
一、单选题
-
1. 已知i为虚数单位,复数z满足 , 则的值为( )A、 B、 C、 D、12. 若数据 , , , 的方差为2,则数据 , , , (a为实数)的方差是( )A、6+a B、8 C、4+a D、123. 设非零向量 , , 满足 , 则( )A、 B、 C、 D、4. 给定下列四个命题,其中真命题是( )A、垂直于同一直线的两条直线相互平行 B、若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行 C、垂直于同一平面的两个平面相互平行 D、若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直5. 中国科协公布的一项调查显示,科技工作者每天平均工作时长为8.6小时,一天最长工作时间为16小时.高学历者每天作时间更长,睡眠缺乏情况严重,博士学历的科技工作者每天平均工作时间最长,为9.29小时.同时,博士和硕士学历的科技工作者每周花在运动上的时间都不足5小时,明显少于其他学历群体,科研人员的健康状况不容忽视.某大型研究所共有职工120人,对他们年龄和身体健康情况进行调查,其结果如下表:
亚健康
健康
合计
35岁以下
40
30
70
35~50岁
27
13
40
50岁以上
8
2
10
现从该研究所职工中任取1人,则下列结论正确的是( )
A、该职工亚健康的概率小于0.6 B、该职工健康的概率大于0.5 C、该职工的年龄在50岁以上的概率大于0.1 D、该职工的年龄不低于35,岁身体健康的概率大于0.16. 《九章算术》是《算经十书》中最重要的一部,成于公元一世纪左右,《九章算术》内容十分丰富,全书总结了战国、秦、汉时期的数学成就,它是一本综合性的历史著作,是当时世界上最简练有效的应用数学,它的出现标志中国古代数学形成了完整的体系.2020年4月,被列入《教育部基础教育课程教材发展中心中小学生阅读指导目录(2020年版)》初中段.书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( ) A、14斛 B、22斛 C、36斛 D、66斛7. 同时抛四枚均匀的硬币,“至少出现一个反面朝上”的概率是( )A、 B、 C、 D、8. 根据如图所示的频率分布直方图,可以估计数据的中位数,众数与平均数,那么这三个数据的60%分位数为( )
A、14斛 B、22斛 C、36斛 D、66斛7. 同时抛四枚均匀的硬币,“至少出现一个反面朝上”的概率是( )A、 B、 C、 D、8. 根据如图所示的频率分布直方图,可以估计数据的中位数,众数与平均数,那么这三个数据的60%分位数为( ) A、12.5 B、13 C、13.5 D、149. 已知a,b,c分别为三个内角A,B,C的对边,a=2,A=45°,若三角形有两解,则b的可能取值是( )A、2 B、2.3 C、3 D、410. 的三个顶点所对的复数分别为 , 复数z满足 ,则的对应点是的( )A、外心 B、内心 C、重心 D、垂心11. 已知 , , , , 若△ABC是直角三角形,则k的值为( )A、-1,-2或8 B、-1,-2或3 C、-2或3 D、-1或312. 如图,四棱锥P-ABCD的底面ABCD为直角梯形, , , , , , 则点P到平面ABCD的距离为( )
A、12.5 B、13 C、13.5 D、149. 已知a,b,c分别为三个内角A,B,C的对边,a=2,A=45°,若三角形有两解,则b的可能取值是( )A、2 B、2.3 C、3 D、410. 的三个顶点所对的复数分别为 , 复数z满足 ,则的对应点是的( )A、外心 B、内心 C、重心 D、垂心11. 已知 , , , , 若△ABC是直角三角形,则k的值为( )A、-1,-2或8 B、-1,-2或3 C、-2或3 D、-1或312. 如图,四棱锥P-ABCD的底面ABCD为直角梯形, , , , , , 则点P到平面ABCD的距离为( )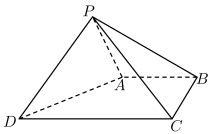 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
13. 若复数与它的共轭复数所对应的向量互相垂直,则 .14. 袋子中有四个小球,分别写有“中、华、民、族”四个字,有放回地从中任取一个小球,直到“中”“华”两个字都取到才停止.用随机模拟的方法估计恰好抽取三次停止的概率,利用电脑随机产生0到3之间取整数值的随机数,分别用 代表“中、华、民、族”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
由此可以估计,恰好抽取三次就停止的概率为.
15. 开封铁塔是宋都开封具有代表性的文物,是文物价值最高、份量最重的宝物之一.1961年,被国务院定为中国首批国家重点保护文物之一.某司机驾车行驶到M处,测得铁塔S在汽车的北偏东15°,与铁塔S相距20公里,汽车继续沿正西方向航行30分钟到达N处后,又测得铁塔在汽车的北偏东45°,则汽车的速度为公里/时. 16. 已知一个球与一个正三棱柱的三个侧面和两个底面都相切,且这个球的体积为 , 那么这个三棱柱的侧面积为 , 体积为 .
16. 已知一个球与一个正三棱柱的三个侧面和两个底面都相切,且这个球的体积为 , 那么这个三棱柱的侧面积为 , 体积为 .三、解答题
-
17. 设z是虚数,是实数,且 .(1)、求z的实部的取值范围;(2)、设 , 求证:u为纯虚数.18. 本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分每小时收费标准为2元(不足1小时的部分按1小时计算).有甲、乙两人相互独立来该租车点租车骑游(各租一车一次),设甲、乙不超过两小时还车的概率分别为;两小时以上且不超过三小时还车的概率分别为;两人租车时间都不会超过四小时.(1)、求出甲、乙两人所付租车费用相同的概率;(2)、求甲、乙两人所付的租车费用之和为4元时的概率.19. 如图,四边形ABCD是正方形,O是正方形的中心,底面ABCD,E是PC的中点,Q是线段PC上的任意一点.求证:
 (1)、平面BDE;(2)、20. 个税专项附加扣除的目的是让大部分人能够减轻纳税负担,对各种收入的人群都能起到一定的减税效果,共涉及子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人、婴幼儿照顾等七项专项附加扣除.某学校具有高级职称、中级职称、初级职称的教师分别有72人,108人,120人,现采用分层随机抽样的方法,从该学校上述教师中抽取25人调查专项附加扣除的享受情况.(1)、应从具有高级职称、中级职称、初级职称的教师中分别抽取多少人?(2)、抽取的25人中,享受至少两项专项附加扣除的教师有6人,分别记为A,B,C,D,E,F.具体享受情况如下表,其中“〇”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
(1)、平面BDE;(2)、20. 个税专项附加扣除的目的是让大部分人能够减轻纳税负担,对各种收入的人群都能起到一定的减税效果,共涉及子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人、婴幼儿照顾等七项专项附加扣除.某学校具有高级职称、中级职称、初级职称的教师分别有72人,108人,120人,现采用分层随机抽样的方法,从该学校上述教师中抽取25人调查专项附加扣除的享受情况.(1)、应从具有高级职称、中级职称、初级职称的教师中分别抽取多少人?(2)、抽取的25人中,享受至少两项专项附加扣除的教师有6人,分别记为A,B,C,D,E,F.具体享受情况如下表,其中“〇”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.(ⅰ)试用所给字母列举出所有可能的抽取结果;
(ⅱ)设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.
A
B
C
D
E
F
子女教育
〇
〇
×
〇
×
〇
继续教育
×
×
〇
×
〇
〇
大病医疗
×
×
×
〇
×
×
住房贷款利息
〇
〇
×
×
〇
〇
住房租金
×
×
〇
×
×
×
赡养老人
〇
〇
×
×
×
〇
婴幼儿照顾
〇
〇
×
×
〇
×

