河南省焦作市2021-2022学年高一下学期数学期末考试试卷

试卷更新日期：2022-07-01 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $z = 2 + i$ ，则 $\frac{\bar{z} - i}{1 + i} =$ （）

A、 $1 - 2 i$ B、 $2 + 2 i$ C、 $2 i$ D、 $- 2 i$

查看试题解析
2. 函数 $y = c o s 2 x + 2 c o s^{2} x$ 的最小值为（）

A、-3 B、-2 C、-1 D、0

查看试题解析
3. 已知则 $p ： x^{2} - 4 x - 12 < 0$ ， $q ： l o g_{2} x < 2$ ， p是q的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 设 $a = l o g_{2} 0.6$ ， $b = s i n 2$ ， $c = {(\frac{2}{5})}^{- \frac{1}{3}}$ ，则a，b，c的大小关系为（）

A、 $a < b < c$ B、 $c < a < b$ C、 $b < c < a$ D、 $a < c < b$

查看试题解析
5. 一个腰长为2的等腰直角三角形绕着它的一条直角边所在的直线旋转 $\frac{π}{4}$ 弧度，形成的几何体的体积为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{π}{2}$ D、 $\frac{2 π}{3}$

查看试题解析
6. 向量 $\vec{a} = (1 ， - 3)$ 在向量 $\vec{b} = (2 ， 4)$ 方向上的投影向量为（）

A、 $(- 1 ， - 2)$ B、 $(1 ， 2)$ C、 $(- 4 ， - 8)$ D、 $(4 ， 8)$

查看试题解析
7. 若函数 $f (x) = l n x + x^{2} - a$ 在区间 $(1 ， e)$ 上存在零点，则实数a的取值范围为（）

A、 $(1 ， e^{2})$ B、 $(1 ， 2)$ C、 $(1 ， e^{2} + 1)$ D、 $(2 ， \frac{2}{e} + 2)$

查看试题解析
8. 已知 $1 + m i (m > 0)$ 是关于 $x$ 的方程 $x^{2} + p x + 2 = 0 (p \in R)$ 在复数范围内的一个根，则 $p + m =$ （）

A、-1 B、-1或-3 C、-3 D、2

查看试题解析
9. 在四面体ABCD中，AB＝CD，且异面直线AB与CD所成的角为50°，M，N分别是边BC，AD的中点，则异面直线MN和AB所成的角为（）

A、25°或50° B、25°或65° C、50° D、65°

查看试题解析
10. 已知定义在R上的奇函数 $f (x)$ 满足 $f (4 - x) = f (x)$ ，且当0≤x≤2时， $f (x) = c o s \frac{π}{4} x + a$ ，则 $f (2022) =$ （）

A、－1 B、0 C、1 D、2

查看试题解析
11. 已知函数 $f (x) = A s i n (ω x + φ) (ω > 0 ， 0 < φ < \frac{π}{2})$ 的部分图像如图所示，点P为 $f (x)$ 图像的最高点，点M，N为 $f (x)$ 的图像与x轴的两个相邻交点，点Q为线段MP与y轴的交点，且MQ＝2QP，△MNP的面积为 $\frac{π}{4}$ ，则函数 $g (x) = l n \frac{3 x}{π}$ 与 $f (x)$ 图像的交点个数为（）

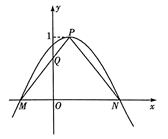A、3 B、2 C、1 D、0

查看试题解析
12. 已知正四棱锥P－ABCD的底面边长为4， $P A = 2 \sqrt{6}$ ， M是棱PA的中点，则四梭锥M－ABCD的外接球的体积为（）

A、 $\frac{9 \sqrt{26}}{2} π$ B、 $\frac{11 \sqrt{26}}{2} π$ C、 $\frac{9 \sqrt{33}}{2} π$ D、 $\frac{11 \sqrt{33}}{2} π$

查看试题解析

二、填空题

13. 已知角 $α$ 的终边经过点 $P (- 3 ， 4)$ ，则 $c o s (\frac{3 π}{2} - α) =$ ．

查看试题解析
14. 已知一组数据 $x_{1} ， x_{2} ， \cdot \cdot \cdot ， x_{n}$ 的平均数 $\bar{x} = 6$ ，方差 $s^{2} = 21$ ，去掉一个数据之后，剩余数据的平均数没有变，方差变为24，则这组数据的个数n＝．

查看试题解析
15. 在正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A A_{1} = 3$ ，过 $A_{1} B$ 且与 $A C_{1}$ 平行的平面交直线 $C C_{1}$ 于点P，则CP＝．

查看试题解析
16. 如图所示， $P C$ 为竖直立于广场上的旗杆，在点 $A$ 、点 $B$ 处分别测得旗杆底端 $C$ 点位于北偏东 $4 5^{∘}$ 方向和北偏西 $3 0^{∘}$ 方向（点 $A$ 、 $B$ 、 $C$ 位于同一水平面内，且点 $B$ 在点 $A$ 的正东方向），从点 $B$ 处仰望旗杆顶端 $P$ 的仰角为 $6 0^{∘}$ ，已知 $A C = 15 m$ ，则旗杆 $P C$ 的高度为 $m$ ．

查看试题解析

三、解答题

17. 已知在平面直角坐标系 $x O y$ 中，向量 $\vec{a} = (3 ， 4)$ ．

(1)、若向量 $\vec{b}$ 满足 $| \vec{b} | = 10$ ，且 $\vec{b} ⊥ \vec{a}$ ，求 $\vec{b}$ 的坐标；

(2)、若向量 $\vec{c}$ 满足 $| \vec{c} | = 2 \sqrt{3}$ ，且 $\vec{a}$ 与 $\vec{c}$ 的夹角为 $\frac{π}{6}$ ，求 $\vec{a} - 2 \vec{c}$ 与 $\vec{a}$ 的夹角的余弦值．

查看试题解析
18. 已知△ABC的内角A，B，C的对边分别为a，b，c且 $a = b c o s A - a c o s B$ ．

(1)、证明：B＝2A；

(2)、若 $b = \sqrt{3} a$ ， c＝2，点E在线段AB上且 $B E = \frac{4}{3}$ ，求CE的长．

查看试题解析
19. 如图所示，在四棱锥P－ABCD中，底面ABCD是边长为4的正方形，PA＝4，PD＝PB，点E在线段PA上，PE＝3EA，BE⊥AD，点F，G分别是线段BC，CD的中点．

(1)、证明：PA⊥平面ABCD；

(2)、求三棱锥P－EFG的体积．

查看试题解析
20. 如图所示，在平行四边形ABCD中，A＝45°， $A B = \sqrt{2} A D$ ， E为AB的中点，将△ADE沿直线DE翻折成△PDE，使平面PDE⊥平面BCD，F为线段PC的中点．

(1)、证明： $B F / /$ 平面PDE；

(2)、已知M为线段DE的中点，求直线MF与平面PDE所成的角的正切值．

查看试题解析
21. 已知函数 $f (x) = 2 a s i n x c o s x + 2 c o s^{2} x - 1$ ， $a > 0$ ．

(1)、求 $f (x)$ 的最小正周期；

(2)、若方程 $f (x) = k$ 在区间 $[0 ， π]$ 上有且仅有两个相异的实数根 $x_{1}$ 、 $x_{2}$ ，且 $x_{1} + x_{2} = \frac{π}{3}$ ，求 $a$ 的值和 $k$ 的取值范围．

查看试题解析
22. 已知函数 $f (x) = e^{x} + k e^{- x}$ 为奇函数．

(1)、求实数k的值；

(2)、若对任意的 $x_{2} \in [0 ， 1]$ ，总存在 $x_{1} \in [t ， + \infty)$ ，使 $e^{| x_{2} - t |} f (x_{1}) \leq 1$ 成立，求实数t的取值范围．

查看试题解析