河南省济源市2021-2022学年高一下学期数学期末教学质量调研试卷

试卷更新日期：2022-07-01 类型：期末考试

进入出卷网下载

一、单选题

1. 已知复数 $\bar{z} = i + 2$ ，则 $z$ 的虚部为（）

A、 $i$ B、-1 C、1 D、 $- i$

查看试题解析
2. 已知向量 $\vec{a} = (- 2 ， \frac{3}{2})$ ， $\vec{2 a} + 3 \vec{b} = (5 ， - 3)$ ，则 $\vec{b} =$ （）

A、 $(- 3 ， 2)$ B、 $(3 ， - 2)$ C、 $(3 ， 0)$ D、 $(9 ， 6)$

查看试题解析
3. 某学校有高中学生900人，其中高一有400人，高二300人，高三200人，采用分层抽样的方法抽取一个容量为45的样本，那么高一、高二、高三各年级抽取的学生人数为

A、30、10、5 B、25、15、5 C、20、15、10 D、15、15、15

查看试题解析
4. 已知某人射击每次击中目标的概率都是0.6，现采用随机模拟的方法估计其3次射击至少2次击中目标的概率 $P$ ．先由计算器产生0到9之间的整数值的随机数，指定0，1，2，3，4，5表示击中目标，6，7，8，9表示未击中目标；因为射击3次，所以每3个随机数为一组，代表3次射击的结果．经随机模拟产生了以下20组随机数：
169 966 151 525 271 937 592 408 569 683

471 257 333 027 554 488 730 863 537 039

据此估计 $P$ 的值为（）

A、0.6 B、0.65 C、0.7 D、0.75

查看试题解析
5. 如图，直角梯形 $O A B C$ 的上、下两底分别为1和2，高为 $\sqrt{2}$ ，则利用斜二测画法所得其直观图的面积为（）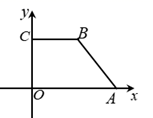

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{3 \sqrt{2}}{8}$ D、 $\frac{3 \sqrt{2}}{4}$

查看试题解析
6. 同时投掷两个质地均匀的骰子，两个骰子的点数至少有一个是偶数的概率为（）

A、 $\frac{7}{36}$ B、 $\frac{11}{36}$ C、 $\frac{11}{12}$ D、 $\frac{3}{4}$

查看试题解析
7. 四边形 $A B C D$ 是正方形，延长 $C D$ 至 $E$ ，使得 $D E = 2 C D$ ，若点 $P$ 为 $B C$ 的中点，且 $\vec{A P} = λ \vec{A B} + μ \vec{A E}$ ，则 $λ + μ =$ （）

A、3 B、2 C、1 D、 $\frac{5}{2}$

查看试题解析
8. 已知 $α$ ， $β$ 是两个不同的平面， $m$ ， $n$ 是两条不同的直线，下列四个命题中正确的是（）

A、如果 $m / / α$ ， $n / / α$ ，那么 $m / / n$ B、如果 $m ⊥ α$ ， $n / / α$ ，那么 $m ⊥ n$ C、如果 $m ⊥ n$ ， $m ⊥ α$ ， $n / / β$ ，那么 $α ⊥ β$ D、如果 $α / / β$ ，直线 $m$ 与 $α$ 所成的角和直线 $n$ 与 $β$ 所成的角相等，那么 $m / / n$

查看试题解析
9. 在 $△ A B C$ 中， $s i n^{2} B \leq s i n^{2} A + s i n^{2} C - s i n A s i n C$ ，则 $B$ 可以是（）

A、 $\frac{π}{6}$ B、 $\frac{π}{2}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
10. 一个口袋内装有大小、形状相同的红色、绿色和蓝色小球各2个，一次任意取出2个小球，则与事件“2个小球都为蓝球”为对立的事件有（）

A、2个小球不全为蓝球 B、2个小球恰有1个蓝球 C、2个小球至少有1个蓝球 D、2个小球都为绿球

查看试题解析
11. 已知 $\vec{A B} ⊥ \vec{A C} ， | \vec{A B} | = \frac{1}{t} ， | \vec{A C} | = t$ ，若 $P$ 点是 $△ A B C$ 所在平面内一点，且 $\vec{A P} = \frac{\vec{A B}}{| \vec{A B} |} + \frac{9 \vec{A C}}{| \vec{A C} |}$ ，则 $\vec{P B} \cdot \vec{P C}$ 的最大值等于（）

A、76 B、78 C、80 D、82

查看试题解析
12. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ， $A = 150 °$ ， $D$ 是边 $B C$ 上一点， $A B ⊥ A D$ ，且 $A D = 1$ ，则 $b + \sqrt{3} c$ 的最小值为（）

A、 $5 + 2 \sqrt{6}$ B、12 C、 $5 + 2 \sqrt{3}$ D、20

查看试题解析

二、填空题

13. 已知 $i$ 是虚数单位，复数 $z = \frac{i^{2021}}{1 - i}$ ，则 $z$ 的共轭复数 $\bar{z}$ 在复平面内对应的点位于第象限．

查看试题解析
14. 在 $△ A B C$ ，其内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，若 $a c o s A c o s B + b c o s^{2} A = a c o s A$ ，则 $△ A B C$ 的形状是．

查看试题解析
15. 甲、乙两人进行羽毛球单打比赛，根据以往比赛的胜负情况知道，每一局甲获胜的概率为 $\frac{2}{3}$ ，乙获胜的概率为 $\frac{1}{3}$ ，如果比赛采用“三局二胜”制（先胜二局者获胜），则前两局打平且甲获胜的概率为．

查看试题解析
16. 已知圆锥底面半径为1，母线长为3，该圆锥内接正方体的体积为．

查看试题解析

三、解答题

17. 在平面直角坐标系 $x O y$ 中，设与 $x$ 轴、 $y$ 轴方向相同的两个单位向量分别为 $\vec{i}$ 和 $\vec{j}$ ， $\vec{O A} = \vec{i} + 2 \vec{j}$ ， $\vec{O B} = 2 \vec{i} + \vec{j}$ ．

(1)、求向量 $\vec{O A}$ 与 $\vec{O B}$ 夹角的余弦值；

(2)、若点 $P$ 是线段 $A B$ 的中点，且向量 $\vec{O P}$ 与 $\vec{O A} + k \vec{O B}$ 垂直，求实数 $k$ 的值．

查看试题解析
18. 一般地，一个大于1的正整数可以表示为两个或两个以上的正整数之和，我们定义：将一个正整数 $n (n > 1)$ 表示为 $k$ 个正整数的和，叫做正整数 $n$ 的 $k$ 拆分，若不考虑拆分部分之间的顺序，称为正整数 $n$ 的无序 $k$ 拆分.例如，4的所有无序2拆分记作：{1，3}，{2，2}．

(1)、写出9的所有无序2拆分；

(2)、从9的所有无序3拆分中任取一个，求“所取拆分中的3个数可以作为 $△ A B C$ 的三边长”的概率.

查看试题解析
19. 记 $△ A B C$ 的内角A，B，C的对边分别为a，b，c，已知 $c = \frac{a}{2} + b c o s A$ .

(1)、求B的大小；

(2)、若 $b = 3 \sqrt{6} ， a + c = 9$ ，求 $△ A B C$ 的面积.

查看试题解析
20. 在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，底面 $A B C D$ 是边长为2的正方形．

(1)、若 $M$ 为 $C C_{1}$ 的中点，试在 $C_{1} D_{1}$ 上确定一点 $N$ ，使得 $A_{1} B / /$ 平面 $B_{1} M N$ ；

(2)、直线 $A_{1} B$ 与平面 $A_{1} D C B_{1}$ 所成的角为 $30 °$ ，求四棱锥 $B - A_{1} D C B_{1}$ 的体积．

查看试题解析
21. 2021年3月18日，位于孝感市孝南区长兴工业园内的湖北福益康医疗科技有限公司正式落地投产，这是孝感市第一家获批的具有省级医疗器械生产许可证资质的企业，也是孝感市首家“一次性使用医用口罩、医用外科口罩”生产企业.在暑期新冠肺炎疫情反弹期间，该公司加班加点生产口罩、防护服，消毒水等防疫物品，保障抗疫一线医疗物资供应，在社会上赢得一片赞誉．在加大生产的同时，该公司狠抓质量管理，不定时抽查口罩质量，该企业质检人员从所生产的口罩中随机抽取了100个，将其质量指标值分成以下六组：[40，50)，[50，60)，[60，70)，......，[90，100]得到如下频率分布直方图．

(1)、求出直方图中 $m$ 的值；

(2)、利用样本估计总体的思想，估计该企业所生产的口罩的质量指标值的平均数和中位数 $($ 同一组中的数据用该组区间中点值作代表，中位数精确到0.01）；

(3)、现规定：质量指标值小于70的口罩为二等品，质量指标值不小于70的口罩为一等品．利用分层抽样的方法从该企业所抽取的100个口罩中抽出5个口罩，在这五个口罩中任意抽取一个，恰好抽中一等品的概率是多少．

查看试题解析
22. 在四棱锥 $S - A B C D$ 中，侧面 $S A B ⊥$ 底面 $A B C D$ ，底面 $A B C D$ 为矩形， $△ S A B$ 为等边三角形， $A B = 1$ ， $B C = \sqrt{3}$ ，点 $E$ 在 $A D$ 上， $A E = 5 D E$ ．

(1)、求证： $C E ⊥ S D$ ；

(2)、求二面角 $E - S B - A$ 的正切值．

查看试题解析