安徽省安庆市岳西县2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

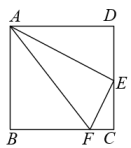
1. 已知二次根式 $\sqrt{2 x + 1}$ ，则x的最小值是（）

A、0 B、-1 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列式子中，与 $\sqrt{2}$ 是同类二次根式的是（）

A、 $\sqrt{7}$ B、 $\sqrt{8}$ C、 $\sqrt{9}$ D、 $\sqrt{10}$

查看试题解析
3. 在以下列数值为边长的三角形中，能构成直角三角形的是（）

A、3.1，4.2，5.3 B、3.2，4.3，5.4 C、3.3，4.4，5.5 D、3.4，4.5，5.6

查看试题解析
4. 下列式子正确的是（）

A、 $\sqrt{2} + \sqrt{3} > \sqrt{5}$ B、 $\sqrt{2} \times \sqrt{3} = \sqrt{5}$ C、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ D、 $\sqrt{2} \times \sqrt{3} < \sqrt{5}$

查看试题解析
5. 已知关于 $x$ 的方程 $x^{2} - 3 x + m = 0$ 的一个根是2，则此方程的另一根为（）

A、0 B、1 C、2 D、3

查看试题解析
6. 用下列一种正多边形，不能用来作平面镶嵌的是（）

A、正三角形 B、正方形 C、正五边形 D、正六边形

查看试题解析
7. 下列命题正确的是（）

A、两条对角线相等的四边形是矩形 B、两条对角线互相垂直的四边形是菱形 C、两条对角线互相垂直平分的四边形是正方形 D、顺次连接任意四边形各边中点所得的四边形是平行四边形

查看试题解析
8. 小华同学所在的801班共有50名学生，省级健康抽测测量了全班学生的身高，小华的身高是1.65米，他通过计算发现该班学生的平均身高也是1.65米，下列说法正确的是（）

A、该班至少有25位同学的身高超过1.65米 B、1.65米是该班学生身高的一般水平 C、该班学生身高的中位数是1.65米 D、该班学生身高出现次数最多的是1.65米

查看试题解析
9. 已知 $m ， n$ 是方程 $x^{2} - 2 x - 1 = 0$ 的两根，则 $m^{2} - m + n$ 的值为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 如图，四边形 $A B C D$ 是矩形，点E在线段 $C B$ 的延长线上，连接 $D E$ 交 $A B$ 于点F， $∠ A E D = 2 ∠ C E D$ ，点G是 $D F$ 的中点，若 $B E = 1$ ， $C D = 3$ ，则 $D F$ 的长为（）

A、8 B、9 C、 $4 \sqrt{2}$ D、 $2 \sqrt{10}$

查看试题解析

二、填空题

11. 若一菱形的两条对角线为 $3 c m ， 4 c m$ ，则这个菱形的周长是cm．

查看试题解析
12. 若整数1至50的方差为 $S_{1}$ ，整数51至100的方差为 $S_{2}$ ，则 $S_{1}$ 与 $S_{2}$ 的大小关系是．

查看试题解析
13. 若n边形恰好有n条对角线，则n= ．

查看试题解析
14.
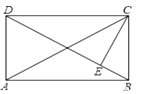
已知：如图，在矩形ABCD中，CE⊥BD，E为垂足，∠DCE：∠ECB=3：1，则∠ACE=.

查看试题解析
15. 已知某个一元二次方程的两根分别是1和-2，则这个方程可以是（填一般形式）．

查看试题解析
16. 在 $▱ A B C D$ 中，边 $A B = 15$ ，对角线 $A C = 13$ ， $B C$ 边的高 $A E = 12$ ，则 $▱ A B C D$ 的周长为．

查看试题解析

三、解答题

17. 已知 $x = \sqrt{2} - 1$ ， $y = \sqrt{2} + 1$ ，求代数式 $x^{2} - y^{2}$ 的值．

查看试题解析
18. 解方程： $(x + 1) (x - 2) = - 1$

查看试题解析
19. 如图，在8×6的网格中，线段 $A B$ 的两个端点分别是网格线的交点．

(1)、请以 $A B$ 为对角线画一个格点矩形（矩形顶点均为网格线的交点）；

(2)、直接写出（1）所画矩形的周长和面积（不用说理）．

查看试题解析
20. 如图，在 $△ A B C$ 中，点D是 $B C$ 的中点，点E在 $A D$ 上，点F在 $A D$ 延长线上，且 $B E / / C F$ ．

(1)、求证：四边形 $B E C F$ 是平行四边形；

(2)、请在 $△ A B C$ 中添加一个条件，使四边形 $B E C F$ 是菱形，并说明理由．

查看试题解析
21. 某商品的生产成本包括固定成本和可变成本，其中固定成本为每年1000元，可变成本逐年增长．已知该商品2019年的可变成本为2000元．

(1)、如果该商品2021年的生产成本为3880元，求可变成本平均每年的增长率；

(2)、若保持可变成本的年增长率不变，请预测2022年该商品的生产成本是多少？

查看试题解析
22. 某九年一贯制学校举行“防溺水知识竞赛”，小学、初中部根据初赛成绩，各选出5名选手组成小学代表队和初中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如下图所示：

(1)、根据图示填写下表：

平均数
中位数
众数
方差
初中部
85
85
70
小学部
80

(2)、小学部的小张说：从高分看，小学部有两个得100分，初中部只有一个得100分，小学部成绩要好于初中部成绩．初中部的小李认为，初中部的成绩要好于小学部，请你帮助小李找出两条理由．

查看试题解析
23. 如图，正方形 $A B C D$ 中，E是 $C D$ 的中点， $E F ⊥ A E$ ，点F在 $B C$ 上．

(1)、求证： $F E$ 平分 $∠ A F C$ ；

(2)、求 $\frac{C F}{B F}$ 的值．

查看试题解析

	平均数	中位数	众数	方差
初中部	85		85	70
小学部		80