云南省昆明市盘龙区2020-2021学年八年级下学期期末考试数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组数中，能构成直角三角形的一组是（）

A、2，3，4 B、3，4，5 C、5，12，16 D、6，8，12

查看试题解析
2. 一元二次方程 $x^{2} - 2 x + 1 = 0$ 的根的情况是（）

A、有两个不等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
3. 将二次函数 $y = x^{2}$ 的图象先向右平移2个单位，再向下平移3个单位，得到的函数图象的表达式是（）

A、 $y = {(x + 2)}^{2} + 3$ B、 $y = {(x + 2)}^{2} - 3$ C、 $y = {(x - 2)}^{2} - 3$ D、 $y = {(x - 2)}^{2} + 3$

查看试题解析
4. 篮球队5名场上队员的身高（单位：cm）分别是：189，191，193，195，196．现用一名身高为192cm的队员换下身高为196cm的队员，与换人前相比，场上队员的身高（）

A、平均数变小，方差变小 B、平均数变小，方差变大 C、平均数变大，方差变小 D、平均数变大，方差变大

查看试题解析
5. 如图，函数 $y = a x$ 和 $y = b x + 5$ 的图象相交于点A，则不等式 $a x ≥ b x + 5$ 的解集为（）

A、 $x \geq 2$ B、 $x \leq 2$ C、 $x \geq 7$ D、 $x \leq 7$

查看试题解析
6. 如图，在矩形ABCD中，AB＝4，BC＝8，对角线AC、BD相交于点O，过点O作OE垂直AC交AD于点E，则DE的长是（）

A、3 B、5 C、2.4 D、2.5

查看试题解析
7. A、B两地相距80km，甲、乙两人沿同一条路从A地到B地，如图 $l_{1}$ ， $l_{2}$ 分别表示甲、乙两人离开A地的距离s（km）与时间t（h）之间的关系．下列说法正确的是（）

A、乙车出发1.5小时后甲才出发 B、两人相遇时，他们离开A地40km C、甲的速度是 $\frac{80}{3}$ km/h D、乙的速度是 $\frac{40}{3}$ km/h

查看试题解析
8. 如图，在四边形 $A B C D$ 中， $A B = A D$ ， $B C = D C$ ， $A C$ ， $B D$ 交于点 $O$ .添加一个条件使这个四边形成为一种特殊的平行四边形，则以下说法错误的是（）

A、添加“ $A B // C D$ ”，则四边形 $A B C D$ 是菱形 B、添加“ $∠ B A D = 90 °$ ”，则四边形 $A B C D$ 是矩形 C、添加“ $O A = O C$ ”，则四边形 $A B C D$ 是菱形 D、添加“ $∠ A B C = ∠ B C D = 90 °$ ”，则四边形 $A B C D$ 是正方形

查看试题解析

二、填空题

9. 关于x的函数 $y = (m + 2) x^{m^{2} - 2}$ 是二次函数，则m的值是.

查看试题解析
10. 若m是方程 $x^{2} - 3 x + 1 = 0$ 的一个根，则 $2 m^{2} - 6 m + 2023$ 的值为．

查看试题解析
11. 一个菱形的两条对角线的长分别为3和6，这个菱形的面积是．

查看试题解析
12. 如图，以直角三角形的三边为边向外作三个正方形A、B、C ．若 $S_{A} = 24$ ， $S_{B} = 16$ ，则 $S_{C} =$ ．

查看试题解析
13. 如图，D，E，F分别是 $△$ ABC各边的中点，AH是BC边上的高，若 $H F = 3$ ，则ED的长为．

查看试题解析
14. 将正方形OEFG放在平面直角坐标系中，O是坐标原点，若点E的坐标为 $(3 ， 2)$ ，则点G的坐标为．

查看试题解析

三、解答题

15. 解下列方程：

(1)、 $x^{2} - x - 2 = 0$ ；

(2)、 $2 x^{2} + 2 x - 1 = 0$ ．

查看试题解析
16. 如图，学校操场边上一块空地（阴影部分）需要绿化，连接AC，测出 $C D = 3$ ， $A D = 4$ ， $B C = 12$ ， $A B = 13$ ， $A D ⊥ C D$ ，求需要绿化部分的面积．

查看试题解析
17. 某商场一种商品的进价为每件30元，售价为每件40元，每天可以销售48件，为尽快减少库存，商场决定降价促销．

(1)、若该商品连续两次下调相同的百分率后售价降至每件32.4元，求两次下降的百分率．

(2)、经调查，若该商品每降价1元，每天可多销售8件，那么每天要想获得504元的利润，每件应降价多少元？

查看试题解析
18. 今年春季开学后，为了庆祝伟大的中国共产党建党100周年，某校开展了“爱祖国·跟党走”的知识网上答题竞赛．现从该校七、八年级中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，共分成四组：A． $80 \leq x < 85$ ， B． $85 \leq x ＜ 90$ ， C． $90 \leq x < 95$ ， D． $95 \leq x \leq 100$ ）
八年级抽取的学生竞赛成绩扇形统计图：
下面给出了部分信息：七年级10名学生的竞赛成绩是：90，81，90，86，99，95，96，100，89，84；八年级10名学生的竞赛成绩在C组中的数据是：90，94，94
【七、八年级抽取的学生竞赛成绩统计表如下】
年级
七年级
八年级
平均数
91
91
中位数
90
b
众数
c
100
方差
52
50.4
根据以上信息，解答下列问题：

(1)、a= ， b= ， c=；

(2)、根据以上数据，你认为该校七、八年级中哪个年级学生掌握的相关知识较好？请说明理由；

(3)、该校七、八年级各200人参加了此次网上答题竞赛活动，估计参加竞赛活动成绩优秀（ $x \geq 90$ ）的学生人数是多少？

查看试题解析
19. 已如，如图，在△ABC中，AB＝AC ， AD是BC边的中线，过点A作BC的平行线，过点B作AD的平行线，两线交于点E ，连接DE交AB于点O ．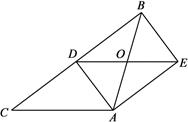

(1)、求证：四边形ADBE是矩形；

(2)、若BC=8，AO= $\frac{5}{2}$ ，求四边形AEBC的面积．

查看试题解析
20. 如图，某校准备一面利用墙，其余三面用篱笆围成一个矩形花圃 $A B C D$ ，已知旧墙可利用的最大长度为 $13 m$ ，篱笆长为 $24 m$ ，设垂直于墙的 $A B$ 边长为 $x m$ .

(1)、若围成的花圃面积为 $70 m^{2}$ 时，求 $B C$ 的长；

(2)、如图，若计划将花圃中间用一道篱笆隔成两个小矩形，且花圃面积为 $78 m^{2}$ ，请你判断能否围成这样的花圃?如果能，求 $B C$ 的长：如果不能，请说明理由.

查看试题解析
21. 如图，已知抛物线 $y = - x^{2} + m x + 3$ 与x轴交于A，B两点，与y轴交于点C，点B的坐标为 $(3 ， 0)$ ．

(1)、求抛物线的解析式及顶点坐标．

(2)、点P是抛物线对称轴l上的一个动点，当 $P A + P C$ 的值最小时，求点P的坐标．

查看试题解析
22. 疫情期间，“地摊经济”成为了社会关注的热门话题.小明从市场得知如下信息：

甲商品

乙商品

进价（元/件）

35

5

售价（元/件）

45

8

小明计划购进甲、乙两种商品共100件进行销售.设小明购进甲商品x件，甲、乙商品全部销售完后获得的利润为y元.

(1)、求出y与x之间的函数关系式；

(2)、小明用不超过2000元资金一次性购进甲，乙两种商品，最多可购进甲商品多少件？

(3)、若购进乙商品的件数不少于甲商品件数的3倍，当购进甲，乙两种商品各多少件时，可使得甲、乙商品全部销售完后获得的利润最大？

查看试题解析
23. 如图，直线BC交x轴于点C，交y轴于点B，与直线 $y = a x$ 交于点A，点A的横坐标为2， $∠ A C O = 45 °$ ， $△$ ABO的面积为1．

(1)、求a的值和直线BC的解析式；

(2)、若直线 $y = a x + m$ 与y轴交于点D，当 $△$ ABD的面积为4时，求m的值；

(3)、若点P为直线BC上的一点，点Q为坐标平面内一点，是否存在符合条件的点P、Q，使点O，A，P，Q为顶点的四边形为菱形，若存在，请直接写出点Q的坐标；若不存在，请说明理由．

查看试题解析

年级	七年级	八年级
平均数	91	91
中位数	90	b
众数	c	100
方差	52	50.4

	甲商品	乙商品
进价（元/件）	35	5
售价（元/件）	45	8