云南省西双版纳傣族自治州2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\sqrt{x - 2021}$ 有意义，实数x的取值范围是（）

A、x≥2021 B、x＞2021 C、x≠2021 D、x≤2021

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{8}$ ÷2＝ $\sqrt{2}$ B、2 $\sqrt{2}$ +3 $\sqrt{3}$ ＝5 $\sqrt{5}$ C、6× $\sqrt{\frac{1}{6}}$ ＝1 D、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$

查看试题解析
3. 某中学八年级（1）班的21名同学参加了学校组织的西双版纳州州情知识竞赛，每个人的最终成绩恰好均不相同．参赛选手小华想知道自己的成绩能否进入前10名，除了要知道自己的成绩外，还需要知道这21名同学成绩的（）

A、平均数 B、中位数 C、方差 D、众数

查看试题解析
4. 一次函数y=2x－2的图象不经过的象限是( )

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 能够判定一个四边形是菱形的条件是（）

A、对角线互相垂直平分 B、对角线互相平分且相等 C、对角线相等且互相垂直 D、对角线互相垂直

查看试题解析
6. 某校三好学生评选的综合成绩由三部分组成：文化课成绩占60%，体育成绩占20%，社会活动成绩占20%，小刚上述三部分成绩依次为90分、85分、92分，则小刚评选三好学生的综合成绩为（）

A、90.8分 B、90.2分 C、89.4分 D、87.4分

查看试题解析
7. 如图，在 $△$ ABC中，D，E分别为AB，AC的中点，F是DE上一点，连接AF和CF，∠AFC＝90°．若DF＝1，AC＝6，则BC的长度为（）

A、5 B、6 C、7 D、8

查看试题解析
8. 如图，正方形ABCD的边长为2cm，动点P从点A出发，在正方形的边上沿A→B→C→D的路径运动到点D停止．设点P的运动路程为x（cm），则下列图象中，能表示 $△$ ADP的面积y（cm²）关于x（cm）的函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 计算： $\sqrt{{(- 3)}^{2}}$ = ．

查看试题解析
10. 如图，已知P是平面直角坐标系中的一点，其坐标为(6，8)，则点P到原点的距离是．

查看试题解析
11. 2022年冬季奥运会将在北京和张家口举办，北京将成为世界上第一个既举办过夏季奥运会，又举办过冬季奥运会的城市．备战此次冬季奥运会，甲、乙两名运动员练习投掷实心球，每人投10次．若两人的平均成绩相同，方差分别为 ${S_{甲}}^{2}$ ＝0.13， ${S_{乙}}^{2}$ ＝0.02，则成绩比较稳定的是（填“甲”或“乙”）运动员．

查看试题解析
12. 将直线y＝x+3向下平移3个单位长度后，所得直线的表达式为．

查看试题解析
13. 如图，在菱形ABCD中，AC，BD两对角线相交于点O．若∠BAD＝60°，BD＝2cm，则菱形ABCD的面积是cm² ．

查看试题解析
14. 如图，在平行四边形ABCD中，DE⊥BC于点E，BF⊥CD于点F，DE和BF相交于点H，BF的延长线与AD的延长线相交于点G．若∠DBC＝45°，现有以下四个说法：①BD＝ $\sqrt{2}$ BE；②∠A＝∠BHE；③△BCF≌△DCE；④AB＝BH，则其中正确的是．

查看试题解析

三、解答题

15. 计算：

(1)、（3 $\sqrt{24}$ ﹣9 $\sqrt{\frac{1}{3}} + \sqrt{48}$ ）÷2 $\sqrt{3}$ ；

(2)、（3+ $\sqrt{5}$ ）（3﹣ $\sqrt{5}$ ）﹣（ $\sqrt{2}$ +1）² ．

查看试题解析
16. 如图，在▱ABCD中，点E是AB边的中点，DE的延长线与CB的延长线交于点F．
求证：BC=BF．

查看试题解析
17. 如图，已知直线y=kx+b经过点A(5，0)，B(1，4).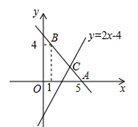

(1)、求直线AB的解析式；

(2)、若直线y=2x-4与直线AB相交于点C，求点C的坐标.

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ A D C = 90 °$ ，若 $C D = 12$ ， $A D = 16$ ， $B C = 15$ .

(1)、求 $A C$ ， $B D$ 的长.

(2)、判断 $△ A B C$ 的形状并说明理由.

查看试题解析
19. 某校招聘一名数学老师，对应聘者分别进行了教学能力、教研能力和组织能力三项测试，其中甲、乙两名应聘者的成绩如下表：（单位：分）
测试项目
应聘者
教学能力
科研能力
组织能力
甲
88
84
86
乙
92
80
74

(1)、若根据三项测试的平均成绩在甲、乙两人中录用一人，谁将被录用？

(2)、根据实际需要，学校将教学、教研和组织能力三项测试得分按7：2：1的比确定每人的最后成绩．若按此成绩在甲、乙两人中录用一人，谁将被录用？

查看试题解析
20. 观察下列式子：
第1个式子： $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \frac{\sqrt{2} - 1}{(\sqrt{2})^{2} - 1} = \frac{\sqrt{2} - 1}{2 - 1} = \sqrt{2} - 1$ ；

第2个式子： $\frac{1}{\sqrt{3} + \sqrt{2}}$ ＝ $\frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})}$ ＝ $\frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3})^{2} - (\sqrt{2})^{2}}$ ＝ $\frac{\sqrt{3} - \sqrt{2}}{3 - 2}$ ＝ $\sqrt{3}$ ﹣ $\sqrt{2}$ ；

第3个式子： $\frac{1}{\sqrt{4} + \sqrt{3}}$ ＝ $\frac{\sqrt{4} - \sqrt{3}}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})}$ ＝ $\frac{\sqrt{4} - \sqrt{3}}{(\sqrt{4})^{2} - (\sqrt{3})^{2}}$ ＝ $\frac{\sqrt{4} - \sqrt{3}}{4 - 3}$ ＝ $\sqrt{4}$ ﹣ $\sqrt{3}$ ；

…

(1)、仿照写出： $\frac{1}{\sqrt{n + 1} + \sqrt{n}} = \sqrt{n + 1} - \sqrt{n}$ 的计算过程；

(2)、根据上述规律求 $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ⋯ + \frac{1}{\sqrt{2021} + \sqrt{2020}}$ 的值．

查看试题解析
21. 网络新词“低头族”是指街头巷尾尤其公交车、地铁上埋头进行手机数字化阅读的人群．某中学课外数学兴趣小组针对“您如何看待手机数字化阅读”进行了随机问卷调查（如图1），并将调查结果绘制成如图2和图3所示的统计图（均不完整）．
请根据统计图中提供的信息，解答下列问题：

(1)、求本次接受调查的总人数，并将两个统计图补充完整；

(2)、求本次调查中五种观点人数的众数、中位数；

(3)、若该市人口总数约为60万，请根据上述信息估计该市市民认同观点D的有多少人．

查看试题解析
22. 抗击疫情，我们在行动．某药店销售A型和B型两种型号的口罩，销售一箱A型口罩可获利120元，销售一箱B型口罩可获利140元．该药店计划一次购进两种型号的口罩共100箱，其中B型口罩的进货量不超过A型口罩的3倍．设购进A型口罩x箱，这100箱口罩的销售总利润为y元．

(1)、求y与x的函数关系式；

(2)、该商店购进A型、B型口罩各多少箱，才能使销售利润最大？最大利润是多少？

(3)、若限定该药店最多购进A型口罩60箱，则这100口罩的销售总利润能否为12540元？请说明理由．

查看试题解析
23. 如图1，在 $△$ ABC中，AB＝AC，AD⊥BC，AN为∠CAM的平分线．

(1)、求证：∠DAN＝90°；

(2)、如图2，过点C作CE∥AD，交AN于点E，求证：四边形ADCE为矩形；

(3)、求当AD和BC满足怎样的数量关系时，四边形ADCE是正方形，并说明理由．

查看试题解析