云南省文山州2020-2021学年八年级下学期期末考试数学试题
试卷更新日期:2022-06-29 类型:期末考试
一、单选题
-
1. 下列四个图形中,是中心对称图形的是( )A、
 B、
B、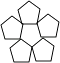 C、
C、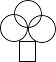 D、
D、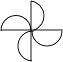 2. 下列计算正确的是( )A、 B、 C、 D、3. 不等式的解集在数轴上表示为( )A、
2. 下列计算正确的是( )A、 B、 C、 D、3. 不等式的解集在数轴上表示为( )A、 B、
B、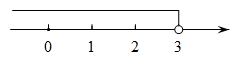 C、
C、 D、
D、 4. 已知一个多边形的内角和是1080°,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形5. 下列说法错误的是( )A、x2+kx+9是完全平方式,则k=±6 B、分别以5cm,12cm,13cm为边长的三角形是直角三角形 C、一组对边相等,另一组对边平行的四边形是平行四边形 D、斜边和一条直角边分别相等的两个直角三角形全等6. 若分式有意义,则x应满足的条件是( )A、 B、 C、 D、7. 如图,在 中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , ,则 的周长为( )
4. 已知一个多边形的内角和是1080°,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形5. 下列说法错误的是( )A、x2+kx+9是完全平方式,则k=±6 B、分别以5cm,12cm,13cm为边长的三角形是直角三角形 C、一组对边相等,另一组对边平行的四边形是平行四边形 D、斜边和一条直角边分别相等的两个直角三角形全等6. 若分式有意义,则x应满足的条件是( )A、 B、 C、 D、7. 如图,在 中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , ,则 的周长为( )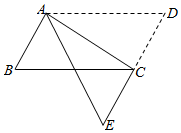 A、12 B、15 C、18 D、218. 按一定规律排列的一组数为: , , , , , ……则第n个数是( )A、 B、 C、 D、
A、12 B、15 C、18 D、218. 按一定规律排列的一组数为: , , , , , ……则第n个数是( )A、 B、 C、 D、二、填空题
-
9. -2的绝对值是10. 因式分解: .11. 如图,在中, , AD是的一条角平分线.若 , 则点D到AB的距离为 .
 12. “m的3倍与2的差不小于0”用不等式表示为 .13. 如图,A,B两地被池塘隔开,小华在地面上确定点O,分取OA、OB的中点C、D,量得 , 则A、B之间的距离是m.
12. “m的3倍与2的差不小于0”用不等式表示为 .13. 如图,A,B两地被池塘隔开,小华在地面上确定点O,分取OA、OB的中点C、D,量得 , 则A、B之间的距离是m. 14. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AC+BD=24,△COD的周长为20,则AB的长为 .
14. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AC+BD=24,△COD的周长为20,则AB的长为 .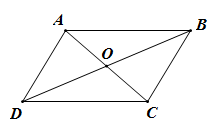
三、解答题
-
15. 解不等式组16. 先化简,再求值: , 其中x=4.17. 云南省出台《关于全面加强新时代大中小学生劳动教育的实施意见》,意见中规定:“在云南省大中小学设立劳动教育必修课程,普通中小学劳动教育课每周不少于个课时”,学校可以组织学生参加校园环境卫生、绿化美化、基地劳作、公务维修等各项劳动.某县教体局为了了解《意见》出台后中小学开设劳动教育课及学生参加劳动时长的情况,特对某中学学生参加劳动教育的情况进行调研,从该校三个年级随机抽取了名学生,对他们一周参加劳动时长进行统计.
数据如下:
整理数据:
劳动时间x(分钟)
人数
分析数据:
平均数
中位数
众数
c
d
根据以上信息,解答下列问题:
(1)、直接填写表格中的值;(2)、若该校现有学生人,估计参加劳动的时间为分钟及以上的有多少人?(3)、请从中位数和众数中选择一个量,说说你对中小学生劳动时长的看法.18. 如图,三个顶点的坐标分别为 , , .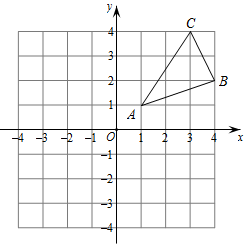
( 1 )请画出向下平移5个单位长度后得到的;
( 2 )请画出关于原点对称的;
( 3 )在y轴上求作一点P,使的周长最小.
19. 2021年1月,中央文明办确定2021—2023年创建周期全国文明城市提名城市名单,云南省共有市县人列,其中,文山市人列,为继续建设文明城市,提升人民生活满意度,某社区计划对一定区域进行绿化.经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的倍,并且在独立完成面积为区域的绿化时,甲队比乙队少用天,求甲、乙施工队每天分别能完成绿化的面积是多少?20. 如图,在平行四边形ABCD中, AC是它的一条对角线,过D,B两点作DE⊥AC,BF⊥AC,垂足分别为E,F,延长DE,BF分别交AB,CD于N,M两点. (1)、求证:四边形BNDM是平行四边形;(2)、已知AE=8,MF=6,求AN的长.21. 某农科所为定点帮扶村免费提供一种优质番茄苗及大棚栽培技术,这种番茄苗早期在温室中生长,长到大约时,移至大棚内,沿插杆继续向上生长,研究表明,天内,这种番茄苗生长的高度与生长时间x(天)之间的关系大致如图所示:
(1)、求证:四边形BNDM是平行四边形;(2)、已知AE=8,MF=6,求AN的长.21. 某农科所为定点帮扶村免费提供一种优质番茄苗及大棚栽培技术,这种番茄苗早期在温室中生长,长到大约时,移至大棚内,沿插杆继续向上生长,研究表明,天内,这种番茄苗生长的高度与生长时间x(天)之间的关系大致如图所示: (1)、求y与x之间的函数关系式;(2)、当这种番茄苗长到大约时,开始开花,试求这种番茄苗移至大棚后,继续生长大约多少天开始开花?22. 近年来,文山州得天独厚的土地、水源、光照等气候条件,吸引了越来越多的人种植特色水果:李子、百香果、苹果、火龙果、草莓、桃子、车厘子…….其中,“黄金”油桃、“山里红”苹果远销北京、上海等一线城市.“某水果专卖店计划购进一批“黄金”油桃和“山里红”苹果共150千克进行销售,购进的“黄金”油桃数量不少于50千克,这两种水果的进价和售价如下表所示:
(1)、求y与x之间的函数关系式;(2)、当这种番茄苗长到大约时,开始开花,试求这种番茄苗移至大棚后,继续生长大约多少天开始开花?22. 近年来,文山州得天独厚的土地、水源、光照等气候条件,吸引了越来越多的人种植特色水果:李子、百香果、苹果、火龙果、草莓、桃子、车厘子…….其中,“黄金”油桃、“山里红”苹果远销北京、上海等一线城市.“某水果专卖店计划购进一批“黄金”油桃和“山里红”苹果共150千克进行销售,购进的“黄金”油桃数量不少于50千克,这两种水果的进价和售价如下表所示:水果
进价(元/千克)
售价(元/千克)
“黄金”油桃
14
18
“山里红”苹果
12
14
设该专卖店购进的“黄金”油桃数量为x千克,售完这批水果获得的总利润为y元,
(1)、求y与x的函数解析式(也称关系式),并直接写出自变量x的取值范围;(2)、由于资金周转问题,该店用于购进这两种水果的总资金不超过2000元,如何进货才能使销售完这批水果获得的总利润最大?最大总利润是多少?23. 在中, , , 点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.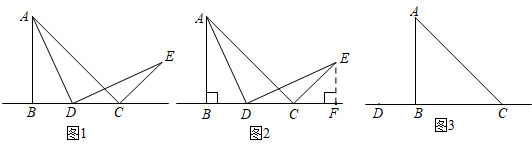 (1)、如果点D在线段BC上运动,如图1:求证:(2)、如果点D在线段BC上运动,请写出AC与CE的位置关系.通过观察、交流,小明形成了以下的解题思路:过点E作交直线BC于F,如图2所示,通过证明 , 可推证等腰直角三角形,从而得出AC与CE的位置关系,请你写出证明过程.(3)、如果点D在线段CB的延长线上运动,利用图3画图分析,(2)中的结论是否仍然成若成立,请证明;若不成立,请说明理由.
(1)、如果点D在线段BC上运动,如图1:求证:(2)、如果点D在线段BC上运动,请写出AC与CE的位置关系.通过观察、交流,小明形成了以下的解题思路:过点E作交直线BC于F,如图2所示,通过证明 , 可推证等腰直角三角形,从而得出AC与CE的位置关系,请你写出证明过程.(3)、如果点D在线段CB的延长线上运动,利用图3画图分析,(2)中的结论是否仍然成若成立,请证明;若不成立,请说明理由.