云南省普洱市2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是以科学家名字命名的，其中是轴对称图形的有（）
赵爽弦图笛卡尔心形线斐波那契螺旋线科克曲线

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列运算正确的是（）

A、 ${(- a^{3})}^{2} = a^{5}$ B、 $\sqrt{2} + \sqrt{8} = \sqrt{10}$ C、 $\sqrt{a^{2}} = a$ D、 $a^{6} \div a^{2} = a^{4}$

查看试题解析
3. 已知 $△ A B C$ 中，a、b、c分别是 $∠ A$ 、 $∠ B$ 、 $∠ C$ 的对边，下列条件中不能判断 $△ A B C$ 是直角三角形的是（）

A、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ B、 $∠ C = ∠ A - ∠ B$ C、 $a^{2} - b^{2} = c^{2}$ D、 $a ： b ： c = 1 ： 1 ： \sqrt{2}$

查看试题解析
4. 甲、乙、丙、丁四个旅游团的游客人数都相等，且每个旅游团游客的平均年龄都是35岁，这四个旅游团游客年龄的方差分别 $S_{甲}^{2} = 6$ ， $S_{乙}^{2} = 1.8$ ， $S_{丙}^{2} = 5$ ， $S_{丁}^{2} = 8$ ，这四个旅游团中年龄相近的旅游团是（）

A、甲团 B、乙团 C、丙团 D、丁团

查看试题解析
5. 某周末，亮亮全家上午8时自驾小汽车从家里出发，到某网红地游玩，该小汽车离家的距离S（千米）与时间t（时）之间的关系如图所示，根据图象提供的有关信息，判断下列说法错误的是（）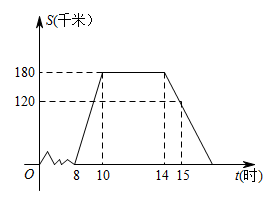

A、景点离亮亮的家180千米 B、10时至14时，小汽车匀速行驶 C、小汽车返程的速度为60千米/时 D、亮亮到家的时间为17时

查看试题解析
6. 如图的阴影部分是两个正方形，图中还有两个直角三角形和一个大正方形，则阴影部分的面积是（）

A、16 B、25 C、144 D、169

查看试题解析
7. 下列关于一次函数 $y = - x + 2$ 的图象性质的说法中，错误的是（）

A、直线与 $x$ 轴交点的坐标是 $(0 ， 2)$ B、与坐标轴围成的三角形面积为 $2$ C、直线经过第一、二、四象限 D、若点 $A (- 1 ， a)$ ， $B (1 ， b)$ 在直线上，则 $a > b$

查看试题解析
8. 如图，在平行四边形 $A B C D$ 上，尺规作图：以点A为圆心， $A B$ 的长为半径画弧交 $A D$ 于点F，分别以点B、F为圆心，以大于 $\frac{1}{2} B F$ 的长为半径画弧交于点P，作射线 $A P$ 交 $B C$ 于点E，连接 $E F$ ．若 $B F = 12$ ， $A B = 10$ ，则线段 $A E$ 的长为（）

A、18 B、17 C、16 D、14

查看试题解析

二、填空题

9. 函数 $y = \sqrt{x - 3}$ 中，自变量x的取值范围是．

查看试题解析
10. 已知流感病毒的直径为0.00000009米，数0.00000009用科学记数法可以表示为．

查看试题解析
11. 若将正比例函数 $y = 2 x$ 的图象向上平移3个单位，得直线 $y = k x + b$ ，则 $k + b$ 的值为.

查看试题解析
12. 如图， $A E ⊥ A B$ ，且 $A E = A B$ ， $B C ⊥ C D$ ，且 $B C = C D$ ，点 $F$ 、 $A$ 、 $G$ 、 $C$ 、 $H$ 在同一条直线上，按照图中所标注的数据，计算图中实线所围成的图形的面积 $S$ 是.

查看试题解析
13. 如图，正方形 $A B C D$ 的边长为4，点E在边 $A B$ 上， $A E = 1$ ，若点P为对角线 $B D$ 上的一个动点，则 $△ P A E$ 周长的最小值是．

查看试题解析
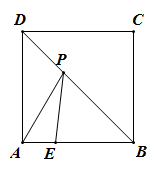14. 如图，△ABC中，∠B=70°，∠C=90°，在射线BA上找一点D，使△ACD为等腰三角形，则∠ADC的度数为．

查看试题解析

三、解答题

15. 计算： ${(\frac{1}{2})}^{- 1} + (π - 3)^{0} - \sqrt{12} \times \frac{\sqrt{3}}{3}$

查看试题解析
16. 如图， $F ， C$ 是线段AD上的两点，且 $A F = C D$ ，点 $E ， F ， G$ 在同一直线上，且 $F ， G$ 分别是 $A C ， A B$ 的中点， $B C = E F .$ 求证： $Δ A B C ≅ Δ D E F$

查看试题解析
17. 先化简，再求值： $(\frac{x^{2} - 2 x + 1}{x^{2} - x} + \frac{x^{2} - 4}{x^{2} + 2 x}) \div \frac{1}{x}$ ，其中 $x = \frac{\sqrt{2}}{2}$ ．

查看试题解析
18. 如图，点O是 $△ A B C$ 内一点，连接 $O B$ 、 $O C$ ，线段 $A B$ 、 $O B$ 、 $O C$ 、 $A C$ 的中点分别为D、E、F、G．

(1)、猜想：四边形 $D E F G$ 是形，并说明理由；

(2)、若M为 $E F$ 的中点， $O M = 1$ ， $∠ O B C + ∠ O C B = 90 °$ ，求线段 $B C$ 的长．

查看试题解析
19. 直线y₁＝﹣x＋3和直线y₂＝kx﹣2分别交y轴于点A、B，两直线交于点C（2，m）.

(1)、求m，k的值；

(2)、求△ABC的面积；

(3)、根照图象直接写出当y₁＞y₂自变量x的取值范围.

查看试题解析
20. 某商店销售A型和B型两种型号的电脑，销售一台A型电脑可获利120元，销售一台B型电脑可获利140元．该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的3倍．设购进A型电脑x台，这100台电脑的销售总利润为y元．

(1)、求y与x的函数关系式，并求出自变量x的取值范围；

(2)、该商店购进A型、B型电脑各多少台，才能使销售利润最大？最大利润是多少？

查看试题解析
21. 4月23日是世界图书日，某校响应号召，鼓励师生利用课余时间广泛阅读．校文学社为了解同学课外阅读情况，抽样调查了部分同学每周用于课外阅读的时间，过程如下：
①数据收集：从全校随机抽取20名同学，调查每周用于课外阅读的时间，数据如表：（单位： $m i n$ ）
30
60
81
50
40
110
130
146
90
100
60
81
120
140
70
81
10
20
100
81
②整理数据：按如下分段整理样本数据并补全表格：
课外阅读时间
$0 \leq x < 40$
$40 \leq x < 80$
$80 \leq x < 120$
$120 \leq x < 160$
等级
D
C
B
A
人数
3
5
8
a
③分析数据：补全下列表格中的统计量：
平均数
中位数
众数
80
b
c
得出结论：

(1)、a= ， b= ， c= ．

(2)、如果该校现有学生3000人，估计等级为“B”的同学有多少名？

(3)、假设平均阅读一本课外书的时间为160分钟，请你选择样本中的一种统计量估算该校学生每人一年（按52周计算）平均阅读多少本课外书？

查看试题解析
22. 如图①，在正方形ABCD中，P是对角线AC上的一点，点E在BC的延长线上，且PE=PB

(1)、求证：△BCP≌△DCP；

(2)、求证：∠DPE=∠ABC；

(3)、把正方形ABCD改为菱形，其它条件不变（如图②），若∠ABC=58°，则∠DPE=　　度．

查看试题解析
23. 在平面直角坐标系中，点 $A (a ， 0)$ ，点 $B (0 ， b)$ ，已知a、b满足 $a^{2} + b^{2} + 8 a + 8 b + 32 = 0$ ．

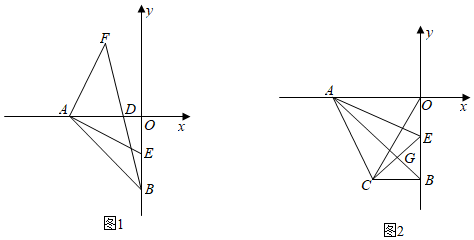(1)、求点A、B的坐标；

(2)、如图1，点E为线段 $O B$ 上一点，连接 $A E$ ，过点A作 $A F ⊥ A E$ ，且 $A F = A E$ ，连接 $B F$ 交x轴于点D，若点F的坐标为 $(- 2 ， c)$ ，求c的值及 $O E$ 的长；

(3)、在（2）的条件下，如图2，过点E作 $E G ⊥ A B$ 于点G，过点B作 $B C / / x$ 轴交 $E G$ 的延长线于点C，连接 $O C$ 、 $A C$ ，试判断 $△ A O C$ 的形状，并说明理由．

查看试题解析

课外阅读时间	$0 \leq x < 40$	$40 \leq x < 80$	$80 \leq x < 120$	$120 \leq x < 160$
等级	D	C	B	A
人数	3	5	8	a

30	60	81	50	40	110	130	146	90	100
60	81	120	140	70	81	10	20	100	81

平均数	中位数	众数
80	b	c