云南省红河哈尼族彝族自治州2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-06-29 类型:期末考试
一、单选题
-
1. 如图是我国几家银行的标志,其中是轴对称图形的有( )
 A、2个 B、3个 C、4个 D、5个2. 若直线y=kx-2经过二、三、四象限,则k的取值范围是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. “龟兔赛跑”新编:兔子和乌龟在上一次比赛中,兔子由于骄傲输给了乌龟.新的一轮比赛开始,兔子汲取教训极力奔跑,一路遥遥领先的兔子在比赛途中捡到一个钱包,为了便于失主尽快找到,兔子焦急地在原地等待,直到钱包被认领.这时,兔子发现乌龟已经远远地跑在了自己的前面,于是它奋起直追,结果拾金不味的兔子与乌龟同时到达终点,用s1 , s2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是( )A、
A、2个 B、3个 C、4个 D、5个2. 若直线y=kx-2经过二、三、四象限,则k的取值范围是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. “龟兔赛跑”新编:兔子和乌龟在上一次比赛中,兔子由于骄傲输给了乌龟.新的一轮比赛开始,兔子汲取教训极力奔跑,一路遥遥领先的兔子在比赛途中捡到一个钱包,为了便于失主尽快找到,兔子焦急地在原地等待,直到钱包被认领.这时,兔子发现乌龟已经远远地跑在了自己的前面,于是它奋起直追,结果拾金不味的兔子与乌龟同时到达终点,用s1 , s2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是( )A、 B、
B、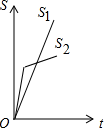 C、
C、 D、
D、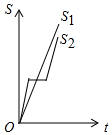 5. 如图,在△ABC中,∠C=90°,AC=BC,BD是∠ABC的平分线,DE⊥AB于点E,若△ADE的周长等于10,则AB的长是( )
5. 如图,在△ABC中,∠C=90°,AC=BC,BD是∠ABC的平分线,DE⊥AB于点E,若△ADE的周长等于10,则AB的长是( ) A、 B、 C、 D、6. 红河州博物馆拟招聘一名优秀讲解员,其中小华笔试、试讲、面试三轮测试得分分别为90分、94分、92分.综合成绩中笔试占30%、试讲占50%、面试占20%,那么小华的最后得分为( )A、分 B、分 C、分 D、分7. 下列命题错误的是( )
A、 B、 C、 D、6. 红河州博物馆拟招聘一名优秀讲解员,其中小华笔试、试讲、面试三轮测试得分分别为90分、94分、92分.综合成绩中笔试占30%、试讲占50%、面试占20%,那么小华的最后得分为( )A、分 B、分 C、分 D、分7. 下列命题错误的是( )①对角线互相垂直且平分的四边形是矩形;②对角线相等的平行四边形是矩形;③有一个角是直角的平行四边形是矩形;④有三个角是直角的四边形是矩形.
A、① B、② C、③ D、④8. 如图,在等腰Rt△ACD中,∠ACD=90°,AC=DC,且AD=2 , 以边AD、AC、CD为直径画半圆,其中所得两个月形图案AGCE和DHCF(图中阴影部分)的面积之和等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 计算:10. 分解因式: .11. 使二次根式有意义的a的取值范围是 .12. 已知正比例函数y=kx的图象经过点(2,6),则k= .13. 若一个多边形的每一个外角都等于40°,则这个多边形的边数是 .14. 已知矩形ABCD中,BE平分∠ABC交矩形的一条边于点E,若BD=10,∠EBD=15°,则AB= .
三、解答题
-
15. 计算: .16. 先化简 , 然后从中选出一个合适的整数作为的值代入求值.17. 如图,在△ABC中,AB>AC,点D在边AB上,且AC=DB,过点D作DE∥AC,并截取AB=DE,且点C、E在AB同侧,连接BE.
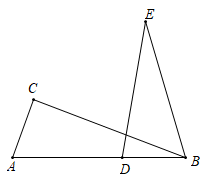
求证:BC=EB.
18. 某校教师前往距离学校10千米的党史学习教育基地参观学习,一部分教师骑自行车先走,过了20分钟后,其余教师乘汽车出发,结果他们同时到达,已知汽车的速度是骑车教师速度的3倍,求骑车教师的速度.19. 如图,将长为2.5米的梯子AB斜靠在墙AO上,BO长0.7米.如果将梯子的顶端A沿墙下滑0.4米,即AM等于0.4米,则梯脚B外移(即BN长)多少米? 20. 为顺利开展“经典咏流传——中国古诗词诵读”活动,需了解七、八年级学生对中国古诗词的掌握情况.学校从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
20. 为顺利开展“经典咏流传——中国古诗词诵读”活动,需了解七、八年级学生对中国古诗词的掌握情况.学校从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:a.八年级成绩频数分布直方图:

b.八年级成绩在这一组的是:
c.七、八年级成绩的平均数、中位数如下表:
年级
平均数
中位数
七年级
八年级
根据以上信息,回答下列问题:
(1)、在这次测试中,八年级学生成绩在分以上(含分)的有人,成绩在这一组数据中的众数是;(2)、在这次测试中,七年级学生甲与八年级学生乙的成绩都是分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;(3)、该校八年级学生有人,假设全部参加此次测试,请估计八年级学生成绩在分以上(含分)的人数.21. 自2020年初新冠肺炎疫情爆发以来,市场对防疫口罩的需求越来越大.某医药公司计划每月生产甲、乙两种型号的防疫口罩共20万只,且所有口罩当月全部售出.其中成本、售价如下表:型号价格(元/只)
项目
甲
乙
成本
售价
设生产甲型号的防疫口罩x万只,所获利润为y元.
(1)、若该公司三月份的销售收入为120万元,求生产甲、乙两种型号的防疫口罩分别是多少万只?(2)、求所获利润y关于x的函数解析式.(3)、如果公司四月份投入成本不超过80万元,应怎样安排甲、乙两种型号防疫口罩的产量,可使该月公司所获利润最大?并求出最大利润.22. 如图,在▱ABCD中,对角线AC、BD交于点O,E是AD上一点,连接EO并延长交BC于点F,连接AF、CE,EF平分∠AEC. (1)、求证:四边形AFCE是菱形.(2)、若∠DAC=60°,EF=4 , 求四边形AFCE的面积.23. 在平面直角坐标系中,矩形纸片AOBC按如图方法放置,点A、B分别在y轴和x轴上,已知OA=2,OB=4,点D在边AC上,且AD=1.
(1)、求证:四边形AFCE是菱形.(2)、若∠DAC=60°,EF=4 , 求四边形AFCE的面积.23. 在平面直角坐标系中,矩形纸片AOBC按如图方法放置,点A、B分别在y轴和x轴上,已知OA=2,OB=4,点D在边AC上,且AD=1.
解答下列问题.
(1)、点C的坐标为 ;(2)、在x轴上有一点E,使得△CDE的周长最短,求出点E的坐标及直线CE的解析式.(3)、在平面直角坐标系内是否存在点P,使得以C、D、P、E为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,说明理由.