云南省大理州祥云县2020-2021学年八年级下学期期末测试卷数学试题
试卷更新日期:2022-06-29 类型:期末考试
一、填空题
-
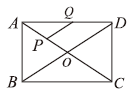
1. 若二次根式有意义,则m的取值范围是 .2. 因式分解: .3. 正六边形的内角和为度.4. 如图,矩形的对角线与相交于点O,P、Q分别为、的中点,若 , 则的长度为 .
 5. 如图,在菱形 中, 、 相交于点O, , 长为4,则菱形 的面积是.
5. 如图,在菱形 中, 、 相交于点O, , 长为4,则菱形 的面积是.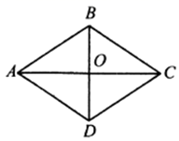 6. 已知 是 的边 上的高,若 , , ,则 的长为.
6. 已知 是 的边 上的高,若 , , ,则 的长为.二、单选题
-
7. 某禽流感病毒的直径大约为 , 这个数字用科学记数法表示为( )A、 B、 C、 D、8. 下列四组线段中,可以组成直角三角形的是( )A、4,5,6 B、3,4,5 C、5,6,7 D、1, ,39. 下列计算正确的是( )A、 B、 C、 D、10. 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
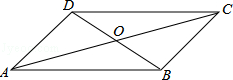 A、AB//DC,AD//BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB//DC,AD=BC11. 若正比例函数的图像经过第一、三象限,则一次函数的图像大致是( )A、
A、AB//DC,AD//BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB//DC,AD=BC11. 若正比例函数的图像经过第一、三象限,则一次函数的图像大致是( )A、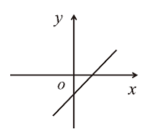 B、
B、 C、
C、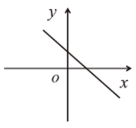 D、
D、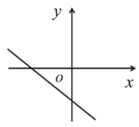 12. 2022年北京张家口将举办冬季奥运会,下表记录了四名短道速滑选手几次选拔赛成绩的平均数 和方差 :
12. 2022年北京张家口将举办冬季奥运会,下表记录了四名短道速滑选手几次选拔赛成绩的平均数 和方差 :甲
乙
丙
丁
平均数 (秒)
52
51
52
51
方差
4.5
4.5
12.5
17.5
根据表中数据,要从中选择出一名成绩好且发挥稳定的运动员,应该选择( )
A、甲 B、乙 C、丙 D、丁13. 在周长为 的正方形 中,点 是 边的中点,点 为对角线 上的一个动点,则 的最小值为( )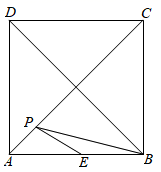 A、2 B、 C、 D、14. 甲、乙两工程队分别同时开挖两条600长的管道,所挖管道长度 (米)与挖掘时间 (天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖2天后,每天挖50米;③甲队比乙队提前3天完成任务;④当 或6时,甲、乙两队所挖管道长度都相差100米,正确的有( )
A、2 B、 C、 D、14. 甲、乙两工程队分别同时开挖两条600长的管道,所挖管道长度 (米)与挖掘时间 (天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖2天后,每天挖50米;③甲队比乙队提前3天完成任务;④当 或6时,甲、乙两队所挖管道长度都相差100米,正确的有( )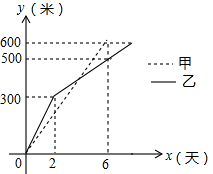 A、①②③ B、①②④ C、②③④ D、①③④
A、①②③ B、①②④ C、②③④ D、①③④三、解答题
-
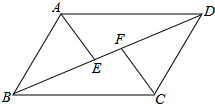
15. 计算:16. 先化简,再求值: ,其中 .17. 如图,在平行四边形ABCD中,E,F分别是对角线BD上的两点,且BE=DF.求证:AE=CF.
 18. 已知直线经过点 ,
18. 已知直线经过点 ,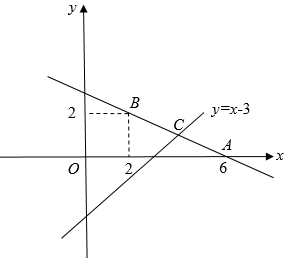 (1)、求直线的解析式(2)、若直线与直线相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式的解集.19. 年月日,漾濞县发生级地震,某市派出两个抢险救灾工程队赶到该县支援,甲工程队承担了米修道路任务,乙工程队比甲工程队多承担了米的道路抢修任务,甲工程队施工速度比乙工程队每小时少修米,结果两工程队同时完成任务.问甲、乙两工程队每小时各抢修道路多少米?20. 为加强师生对“新型冠状病毒肺炎防护知识”的了解,某校精心制作了一套“新冠肺炎防控知识”测试卷,并组织全校师生进行测试,测试卷共道题,每道题分,测试成绩分为A(分数),B(分数),C(分数),D(分数)四个等级,测试结束后,统计老师从全体师生中随机抽取人的成绩(单位:分),收集数据如下:
(1)、求直线的解析式(2)、若直线与直线相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式的解集.19. 年月日,漾濞县发生级地震,某市派出两个抢险救灾工程队赶到该县支援,甲工程队承担了米修道路任务,乙工程队比甲工程队多承担了米的道路抢修任务,甲工程队施工速度比乙工程队每小时少修米,结果两工程队同时完成任务.问甲、乙两工程队每小时各抢修道路多少米?20. 为加强师生对“新型冠状病毒肺炎防护知识”的了解,某校精心制作了一套“新冠肺炎防控知识”测试卷,并组织全校师生进行测试,测试卷共道题,每道题分,测试成绩分为A(分数),B(分数),C(分数),D(分数)四个等级,测试结束后,统计老师从全体师生中随机抽取人的成绩(单位:分),收集数据如下:.
根据以上数据,整理绘制了如下不完整的条形统计图:

根据以上提供的信息,解答下列问题:
(1)、补全条形统计图;(2)、分析数据,补充完成下列表格;平均数
众数
中位数
(3)、为了让学生重视新冠肺炎防控知识的学习,学校将对测试成绩在A等级的学生进行表扬,该校共有名学生,请估计会有多少名学生得到表扬?21. 如图,平行四边形 中, ,过点D作 交 的延长线于点E , 点M为 的中点,连结 . (1)、求证:四边形 是矩形;(2)、若 ,且 ,求四边形 的周长.22. 某商店销售A型和B型两种型号的电脑,销售一台A型电脑可获利元,销售一台B型电脑可获利150元.该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的3倍.设购进A型电脑x台,这台电脑的销售总利润为y元.(1)、求y与x的函数关系式;(2)、该商店购进A型、B型电脑各多少台,才能使销售利润最大?最大利润是多少?23. 如图,在矩形中,点C在x轴上,点A在y轴上,点B的坐标是 . 矩形沿直线折叠,使得点A落在对角线上的点E处,且直线与轴分别交于点 .
(1)、求证:四边形 是矩形;(2)、若 ,且 ,求四边形 的周长.22. 某商店销售A型和B型两种型号的电脑,销售一台A型电脑可获利元,销售一台B型电脑可获利150元.该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的3倍.设购进A型电脑x台,这台电脑的销售总利润为y元.(1)、求y与x的函数关系式;(2)、该商店购进A型、B型电脑各多少台,才能使销售利润最大?最大利润是多少?23. 如图,在矩形中,点C在x轴上,点A在y轴上,点B的坐标是 . 矩形沿直线折叠,使得点A落在对角线上的点E处,且直线与轴分别交于点 .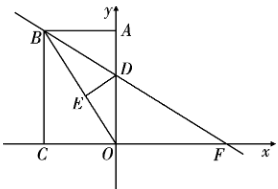 (1)、求线段的长;(2)、求的面积;(3)、在x轴上是否存在点使得以为顶点的四边形是平行四边形?若存在,请求出满足条件的M点的坐标;若不存在,请说明理由.
(1)、求线段的长;(2)、求的面积;(3)、在x轴上是否存在点使得以为顶点的四边形是平行四边形?若存在,请求出满足条件的M点的坐标;若不存在,请说明理由.