安徽省黄山市黟县2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中： $\sqrt{2}$ 、 $\sqrt{3 \frac{1}{2}}$ 、 $\sqrt{12}$ 、 $\sqrt{0.2}$ ， $\sqrt{9}$ ，最简二次根式的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
2. 要使二次根式 $\frac{\sqrt{2 x + 3}}{x - 1}$ 有意义，x的取值范围是（）

A、x≠ $1$ B、 $x \geq - \frac{3}{2}$ C、 $x \geq \frac{3}{2}$ D、 $x \geq - \frac{3}{2}$ 且 $x \neq 1$

查看试题解析
3. 下列各式成立的是（）

A、 $3 \sqrt{2} - \sqrt{2} = 3$ B、 $\sqrt{2 + \frac{2}{3}} = 2 \sqrt{\frac{2}{3}}$ C、 $\frac{\sqrt{18} - \sqrt{8}}{2} = \sqrt{9} - \sqrt{4} = 1$ D、 $\sqrt{18} - \sqrt{\frac{2}{9}} = \frac{7}{3} \sqrt{2}$

查看试题解析
4. 下面四个命题：①对顶角相等；②同旁内角互补，两直线平行；③全等三角形的对应角相等；④如果两个实数的平方相等，那么这两个实数相等，其中逆命题是真命题的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
5. △ABC的三边分别为下列各组值，其中不是直角三角形三边的是（）

A、a=41，b=40，c=9 B、a=1.2，b=1.6，c=2 C、a= $\frac{1}{2}$ ， b= $\frac{1}{3}$ ， c= $\frac{1}{4}$ D、a= $\frac{3}{5}$ ， b= $\frac{4}{5}$ ， c=1

查看试题解析
6. 如图，平行四边形ABCD中，E，F是对角线BD上的两点，如果添加一个条件使△ABE≌△CDF，则添加的条件不能是（）

A、AE=CF B、BE=FD C、BF=DE D、∠1=∠2

查看试题解析
7. 若 $x = \sqrt{3} + 1 ， y = \sqrt{3} - 1$ ，则x²－y²的值为（）

A、 $4 \sqrt{3}$ B、 $2 \sqrt{3}$ C、0 D、2

查看试题解析
8. △ABC中，AB＝15，AC＝13，BC边上的高AD＝12，则△ABC的周长为（）

A、42 B、33 C、42或32 D、37或33

查看试题解析
9. 勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90^O ， AB=3，AC=4，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为（）

A、90 B、100 C、110 D、121

查看试题解析
10. 如图，AD为等边△ABC边BC上的高，AB＝4，AE＝1，P为高AD上任意一点，则EP＋BP的最小值为（）

A、 $2 \sqrt{3}$ B、 $\sqrt{13}$ C、 $\sqrt{10}$ D、 $\sqrt{15}$

查看试题解析

二、填空题

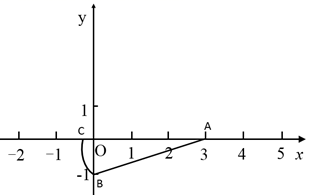
11. 已知四边形 $A B C D$ 是周长为32的平行四边形，若 $A B = 6$ ，则 $B C =$ .

查看试题解析
12. 如图，x轴、y轴上分别有两点 $A (3 ， 0)$ 、 $B (0 ， - 1)$ ，以点A为圆心， $A B$ 为半径的弧交x轴负半轴于点C，则点C的坐标为.

查看试题解析
13. 在实数范围内分解因式：x²﹣7＝.

查看试题解析
14. 已知m、n分别表示 $5 - \sqrt{7}$ 的整数部分和小数部分，求 $m^{2} + (3 + \sqrt{7}) n$ ＝．

查看试题解析
15. 如图是一个外轮廓为矩形的机器零件平面示意图，根据图中的尺寸（单位： $m m$ ），计算两圆孔中心A和B的距离为mm．

查看试题解析
16. 在《九章算术》中有一个问题（如图)：今有竹高一丈，末折抵地，去本三尺，问折者高几何?它的意思是：一根竹子原高一丈（ $10$ 尺)，中部一处折断，竹梢触地面处离竹根 $3$ 尺，试问折断处离地面尺．

查看试题解析
17. 如图，在等边三角形△ABC中，射线AD四等分∠BAC交BC于点D，其中∠BAD＞∠CAD，则 $\frac{C D}{B D}$ ＝．

查看试题解析
18. 观察下列各式：
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1 \times 2} = 1 + (1 - \frac{1}{2})$ ，

$\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2 \times 3} = 1 + (\frac{1}{2} - \frac{1}{3})$ ，

$\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3 \times 4} = 1 + (\frac{1}{3} - \frac{1}{4})$ ，

……

请利用你发现的规律，计算：

$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} + \dots +$

$\sqrt{1 + \frac{1}{2020^{2}} + \frac{1}{2021^{2}}}$

其结果为

查看试题解析

三、解答题

19. 计算

(1)、 $\sqrt{12} - 3 \sqrt{\frac{1}{3}} + (\sqrt{2} - \sqrt{3}) (\sqrt{2} + \sqrt{3})$

(2)、 $\sqrt{8} \div \sqrt{2} - 4 \times \sqrt{\frac{1}{2}} \times (\sqrt{2} - 1)^{0} + (\sqrt{2} + 1)^{2}$

查看试题解析
20.

(1)、已知： $y = \frac{\sqrt{x^{2} - 4} + \sqrt{4 - x^{2}}}{x - 2} + 3$ ，求yx．

(2)、已知 $x = \sqrt{3} + \sqrt{2} ， y = \sqrt{3} - \sqrt{2}$ ，求x²y+xy²的值．

查看试题解析
21. 如图，四边形ABCD中AC、BD相交于点O，延长AD至点E，连接EO并延长交CB的延长线于点F，∠E＝∠F，AD＝BC．

(1)、求证：O是线段AC的中点：

(2)、连接AF、EC，证明四边形AFCE是平行四边形．

查看试题解析
22. 如图，△ABC的周长为19，点D，E在边BC上，∠ABC的平分线垂直于AE，垂足为N，∠ACB的平分线垂直于AD，垂足为M，若BC=7，求MN的长度．

查看试题解析
23. 如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，分别按下列要求画以格点为顶点三角形和平行四边形．

(1)、三角形三边长为4，3 $\sqrt{2}$ ， $\sqrt{10}$ ；

(2)、平行四边形有一锐角为45°，且面积为6．

查看试题解析
24. 阅读下列一段文字，然后回答下列问题．
已知平面内两点 M（x1，y1）、N（x2，y2），则这两点间的距离可用下列公式计算： MN= $\sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ ．

例如：已知 P（3，1）、Q（1，﹣2），则这两点间的距离 PQ= $\sqrt{{(3 - 1)}^{2} + {(1 + 2)}^{2}}$ = $\sqrt{13}$ ．

特别地，如果两点 M（x1，y1）、N（x2，y2）所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴，那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨．

(1)、已知 A（1，2）、B（﹣2，﹣3），试求 A、B 两点间的距离；

(2)、已知 A、B 在平行于 x 轴的同一条直线上，点 A 的横坐标为 5，点 B 的横坐标为﹣1，
试求 A、B 两点间的距离；

(3)、已知△ABC 的顶点坐标分别为 A（0，4）、B（﹣1，2）、C（4，2），你能判定△ABC 的形状吗？请说明理由．

查看试题解析