安徽省淮南市田家庵区2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中 $\sqrt{2} ， \sqrt[3]{5} ， - \sqrt{3} ， \sqrt{- 7} ， \sqrt{x^{2} + 1}$ 一定是二次根式的有（）个．

A、2 B、3 C、4 D、5

查看试题解析
2. 若平行四边形中两个相邻内角的度数之比为 $1 ： 3$ ，则其中较小的内角是（）

A、45° B、30° C、60° D、36°

查看试题解析
3. 为调查某班学生每天使用零花钱的情况，张华随机调查了30名同学，结果如下：

每天使用零花钱（单位：元）

1

2

3

4

5

人数

2

5

8

9

6

则这30名同学每天使用的零花钱的众数和中位数分别是（）

A、4，3 B、4，3.5 C、9，3.5 D、9，8.5

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{3} \times \sqrt{2} = \sqrt{5}$ C、 $\frac{\sqrt{3}}{\sqrt{2}} = 1$ D、 $(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2}) = 1$

查看试题解析
5. 如图，在 $4 \times 4$ 的网格中，每个小正方形的边长均为1，点A，B，C都在格点上， $A D ⊥ B C$ 于点D，则AD的长为（）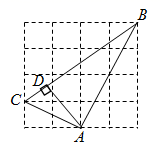

A、1 B、2 C、 $\frac{3}{2}$ D、 $\frac{7}{3}$

查看试题解析
6. 一组数据3，4，4，5，若添加一个数4，则发生变化的统计量是（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
7. 如图所示，在平行四边形 $A B C D$ 中， $A C$ 与 $B D$ 相交于点O，过点O作直线m交线段 $A B$ 于点E，交线段 $C D$ 于点F.则图中共有几对全等三角形（）

A、4 B、5 C、6 D、7

查看试题解析
8. 在 $△ A B C$ 中，若 $A B = 3 ， B C = 5 ， A C = \sqrt{34}$ ，则下列说法正确的是（）

A、 $△ A B C$ 是锐角三角形 B、 $△ A B C$ 是直角三角形且 $∠ C = 90 °$ C、 $△ A B C$ 是钝角三角形 D、 $△ A B C$ 是直角三角形且 $∠ B = 90 °$

查看试题解析
9. 如图，在矩形 $A B C D$ 中， $A B = 3$ ， $A D = 4$ ， $∠ A B C$ 的平分线 $B E$ 交 $A D$ 于点E．点F，G分别是 $B C$ ， $B E$ 的中点，则 $F G$ 的长为（）

A、 $2$ B、 $\frac{5}{2}$ C、 $\frac{\sqrt{10}}{2}$ D、 $\frac{3 \sqrt{2}}{2}$

查看试题解析
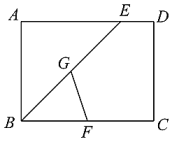10. 如图，甲、乙两汽车从A城出发前往B城，在整个行程中，汽年离开A城的距离y与时间t的对应关系如图所示．下列的结论：①A，B两城相距 $300 k m$ ；②行程中甲、乙两车的速度比为 $2 ： 3$ ；③乙车于7：20追上甲车；④9：00 时，甲、乙两车相距 $60 k m$ ．其中正确的有（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 小明上学期数学的平时成绩80分，期中成绩90分，期末成绩85分，若学期总评成绩按平时：期中：期末＝3：3：4计算，则小明上学期数学的总评成绩是分．

查看试题解析
12. 一直角三角形的两边长分别为5和12，则第三边的长是．

查看试题解析
13. 已知菱形 $A B C D$ 中，对角线 $A C = 3$ ， $B D = 4$ ，则该菱形 $A B$ 与 $C D$ 之间的距离是．

查看试题解析
14. 已知 $y = \sqrt{3 - x} + \sqrt{x - 3} - 2$ ，则 $y^{x} =$ ．

查看试题解析
15. 如图，在平面直角坐标系中，直线 $y = - \frac{3}{4} x + 3$ 交 $x$ 轴于点A，交y轴于点B，以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则直线BC的解析式为.

查看试题解析
16. 如图，在 $▱ A B C D$ 中，点E是AD边上的一点，CD=CE，将 $△ C D E$ 沿CE翻折得到 $△ C E F$ ，若∠B=55°.那么 $∠ B C F$ 的度数为.

查看试题解析
17. 直线 $l_{1} ： y = k_{1} x + b$ 与直线 $l_{2} ： y = k_{2} x$ 在同一平面直角坐标系中的图象如图所示，直线 $l_{1} ： y = k_{1} x + b$ 交x轴于点 $(- 3 ， 0)$ ，则关于x的不等式 $k_{2} x < k_{1} x + b < 0$ 的解集为．

查看试题解析
18. 如图，点P是 $Rt △ A B C$ 中斜边 $A C$ （不与A，C重合）上一动点，分别作 $P M ⊥ A B$ 点M，作 $P N ⊥ B C$ 于点N，点O是 $M N$ 的中点，若 $A B = 6$ ， $B C = 8$ ，当点P在 $A C$ 上运动时，则 $B O$ 的最小值是.

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{27} - \sqrt{12} + \sqrt{\frac{1}{3}} + \sqrt[3]{8}$ ；

(2)、 $(2 \sqrt{3} + \sqrt{15}) (\sqrt{15} - 2 \sqrt{3})$ ．

查看试题解析
20. 某校检测学生跳绳水平，抽样调查了部分学生的“1分钟跳绳”成绩，并制成了下面的频数分布直方图（每小组含最小值，不含最大值）和扇形图

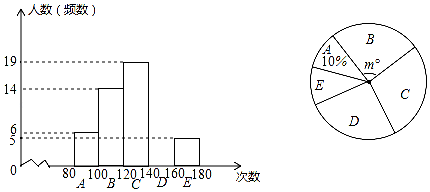(1)、D组的人数是人，补全频数分布直方图，扇形图中m＝；

(2)、本次调查数据中的中位数落在组；

(3)、如果“1分钟跳绳”成绩大于或等于120次为优秀，那么该校4500名学生中“1分钟跳绳”成绩为优秀的大约有多少人？

查看试题解析
21. 如图，在平面直角坐标系中，直线 $y_{1} = 2 x$ 和直线 $y_{2} = - x + m$ 相交于点A，且点A的纵坐标为2，点B在线段OA上（不与O、A重合），过点B作BC//x轴（自己完成）交直线 $y_{2} = - x + m$ 于点C.

(1)、求m的值；

(2)、若线段BC=2，请直接写出点B的坐标.

查看试题解析
22. 某花农要将规格相同的800棵平安树运往A，B，C三地销售，要求运往C地的棵数是运往A地棵数的3倍，各地的运费如下表所示：

A地

B地

C地

运费（元/棵）

10

20

15

(1)、设运往A地的平安树x（棵），总运费为y（元），试写出y与x的函数关系式.

(2)、若要求运往A地的平安树不超过运往B地的平安树，且总运费不超过14000元，问当运往A地的平安树多少棵时，总运费才最省？

查看试题解析
23. 已知，在 $▱ A B C D$ 中， $A E ⊥ B C$ 于点E， $A F ⊥ C D$ 于点F，且 $A E = A F$ .

(1)、如图1，当EC=4，AE=8时，求 $▱ A B C D$ 的对角线BD的长.

(2)、如图2，若点M为CD的中点，连接EM，AM.求证：AM=EM.

查看试题解析

每天使用零花钱（单位：元）	1	2	3	4	5
人数	2	5	8	9	6

	A地	B地	C地
运费（元/棵）	10	20	15