安徽省淮北市濉溪县2020-2021学年八年级下学期期末考试数学试卷

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，关于x的一元二次方程是（）

A、x²﹣x（x+3）＝0 B、ax²+bx+c＝0 C、x²﹣2x﹣3＝0 D、x²﹣2y﹣1＝0

查看试题解析
2. 下列计算正确的是（　　）

A、 $\sqrt{{(- 3)}^{2}}$ ＝﹣3 B、﹣ $\sqrt{0.36}$ ＝﹣0.6 C、 $\sqrt{36}$ ＝±6 D、 $\sqrt[3]{- 5}$ ＝ $\sqrt[3]{5}$

查看试题解析
3. 已知关于x的一元二次方程 $x^{2} - (2 m - 1) x + m^{2} = 0$ 有实数根，则m的取值范围是（）

A、 $m \neq 0$ B、 $m \leq \frac{1}{4}$ C、 $m < \frac{1}{4}$ D、 $m > \frac{1}{4}$

查看试题解析
4. 已知两条线段的长分别为 $\sqrt{2}$ cm、 $\sqrt{3}$ cm，那么能与它们组成直角三角形的第三条线段是（）

A、1cm或 $\sqrt{5}$ cm B、1cm C、 $\sqrt{5}$ cm D、5cm

查看试题解析
5. 有x支球队参加篮球比赛，每两队之间都比赛一场，共比赛了21场，则下列方程中正确的是（）

A、x（x﹣1）＝21 B、x（x﹣1）＝42 C、x（x+1）＝21 D、x（x+1）＝42

查看试题解析
6. 一个多边形所有内角与外角的和为1260°，则这个多边形的边数是（）

A、5 B、7 C、8 D、9

查看试题解析
7. 我们知道方程x²＋2x-3＝0的解是x₁＝1，x₂＝-3，现给出另一个方程(2x＋3)²＋2(2x＋3)-3＝0，它的解是(　　).

A、x₁＝1，x₂＝3 B、x₁＝1，x₂＝-3 C、x₁＝-1，x₂＝3 D、x₁＝-1，x₂＝-3

查看试题解析
8. 为了了解某校学生的课外阅读情况，随机抽查了10名学生一周阅读用时数，结果如下表，则关于这10名学生周阅读所用时间，下列说法中正确的是（）
周阅读用时数（小时）
4
5
8
12
学生人数（人）
3
4
2
1

A、中位数是6.5 B、众数是12 C、平均数是3.9 D、方差是6

查看试题解析
9. 如图，赵爽弦图是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为 $a$ 和 $b$ .若 $a b = 8$ ，大正方形的边长为5，则小正方形的边长为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $B C = 4$ ，点P为 $A B$ 边上任意一点过点P分别作 $P E ⊥ A C$ 于点E， $P F ⊥ B C$ 于点F，则线段 $E F$ 的最小值是（）

A、2 B、2.4 C、3 D、4

查看试题解析

二、填空题

11. $\sqrt{27}$ 与最简二次根式 $\sqrt{m - 1}$ 是同类二次根式，则m= ．

查看试题解析
12. 一个多边形的内角和是720°，则这个多边形的对角线共有条．

查看试题解析
13. 在环保整治行动中，某市环保局对辖区内的单位进行了抽样调查，他们的综合得分如下：95，85，83，95，92，90，96，则这组数据的中位数是，众数是．

查看试题解析
14. 在三角形纸片ABC中， $∠ A = 9 0^{°}$ ， $∠ C = 3 0^{°}$ ， $A C = 30 c m$ .将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD（如图1），剪去 $Δ C D E$ 后得到双层 $Δ B D E$ （如图2），再沿着边 $Δ B D E$ 某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形.则所得平行四边形的周长为cm.

查看试题解析
15. 若把代数式 $x^{2} - 2 x - 2$ 化成 ${(x + m)}^{2} + k$ 的形式，其中m，k为常数，则 $m + k =$ ．

查看试题解析

三、解答题

16.

(1)、计算 $\sqrt{18} - \sqrt{\frac{9}{2}} + {(\sqrt{3} - 2)}^{0} + \sqrt{{(1 - \sqrt{2})}^{2}}$ ；

(2)、解方程： $x^{2} + 4 x - 5 = 0$ ．

查看试题解析
17. 已知 $△ A B C$ 的三边长为a，b，c，且 $a + b = 7$ ， $a b = 1$ ， $c^{2} = 47$ ，试判断 $△ A B C$ 的形状，并说明理由．

查看试题解析
18. 阅读并完成下面问题：
① $\frac{1}{1 + \sqrt{2}} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；
② $\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；
③ $\frac{1}{\sqrt{5} + 2} = \frac{1 \times (\sqrt{5} - 2)}{(\sqrt{5} + 2) (\sqrt{5} - 2)} = \sqrt{5} - 2$ ； …

(1)、填空： $\sqrt{7} + \sqrt{6}$ 的倒数为． $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ （n为正整数）的值为．

(2)、计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \cdot \cdot \cdot + \frac{1}{\sqrt{100} + \sqrt{99}}$ ．

查看试题解析
19. 已知 $x_{1}$ ， $x_{2}$ 是关于x的方程 $x^{2} + 2 (m - 2) x + m^{2} + 4 = 0$ 的两个根，是否存在实数m使 $x_{1}^{2} + x_{2}^{2} - x_{1} x_{2} = 21$ 成立？若存在，求出m的值；若不存在，说明理由.

查看试题解析

20. 我市某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.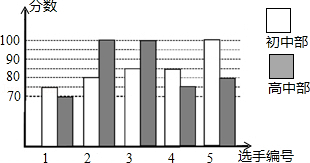

(1)、根据图示填写下表；

	平均数（分）	中位数（分）	众数（分）
初中部		85
高中部	85		100

(2)、结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；

(3)、计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.

查看试题解析

21. 如图，在四边形ABCD中，∠DAB＝∠BCD＝90°，点E是BD上任意一点，点O是AC的中点，AF∥EC交EO的延长线于点F，连接AE，CF.

(1)、判断四边形AECF是什么四边形，并证明；

(2)、若点E是BD的中点，四边形AECF又是什么四边形？说明理由．

查看试题解析
22. 某工厂计划从今年1月份起，每月生产收入为22万元，但生产过程中会引起环境污染，将会受到环保部门的处罚，每月罚款2万元．如果投资111万元治理污染，从1月份开始，每月不但不受处罚，还可降低生产成本，使1月至3月生产收入以相同的百分率逐月增长，3月份以后，每月生产收入稳定在3月份的水平．经测算，投资治污后，1月份生产收入为25万元，3月份生产收入为36万元．

(1)、求投资治污后，2月、3月每月生产收入增长的百分率；

(2)、如果把利润看作是每月生产收入的总和减去治理污染的投资或环保部门的罚款，试问治理污染多少个月后，所投资金开始见成效(即治污后所获得利润不少于不治污情况下所获利润)?

查看试题解析

周阅读用时数（小时）	4	5	8	12
学生人数（人）	3	4	2	1