安徽省淮北市2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

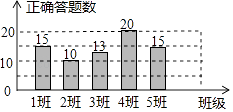
1. 下列二次根式中属于最简二次根式的是（）

A、 $2 \sqrt{x y}$ B、 $\sqrt{\frac{a b}{2}}$ C、 $\sqrt{0.5}$ D、 $\sqrt{2 x^{2}}$

查看试题解析
2. 如果2是方程x²-3x+k=0的一个根，则常数k的值为（）．

A、2 B、1 C、-1 D、-2

查看试题解析
3. 某校举行“汉字听写比赛”，5个班级代表队的正确答题数如图．这5个正确答题数所组成的一组数据的中位数和众数分别是（）

A、10，15 B、13，15 C、13，20 D、15，15

查看试题解析
4. 若一个正n边形的每个内角为144°，则这个正n边形的所有对角线的条数是（）

A、7 B、10 C、35 D、70

查看试题解析
5. 一元二次方程 $x^{2} - 4 x - 1 = 0$ 配方后可化为（）

A、 ${(x + 2)}^{2} = 3$ B、 ${(x + 2)}^{2} = 5$ C、 ${(x - 2)}^{2} = 3$ D、 ${(x - 2)}^{2} = 5$

查看试题解析
6. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若（a+b）²=21，大正方形的面积为13，则小正方形的面积为（）

A、3 B、4 C、5 D、6

查看试题解析
7. 若α、β为方程2x²-5x-1=0的两个实数根，则 $2 α^{2} + 3 α β + 5 β$ 的值为（）

A、-13 B、12 C、14 D、15

查看试题解析
8. 如图，在平行四边形ABCD中，∠C=120°，AD=2AB=4，点H、G分别是边CD、BC上的动点.连接AH、HG，点E为AH的中点，点F为GH的中点，连接EF，则EF的最大值与最小值的差为（）

A、1 B、 $\sqrt{3} - 1$ C、 $\frac{\sqrt{3}}{2}$ D、 $2 - \sqrt{3}$

查看试题解析
9. 如图，正方形 $A B C D$ 的边长为2，其面积标记为 $S_{1}$ ；以 $C D$ 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为 $S_{2}$ ；…；按照此规律作下去，则 $S_{2021}$ 的值为（）

A、 ${(\frac{1}{2})}^{2016}$ B、 ${(\frac{\sqrt{2}}{2})}^{2017}$ C、 ${(\frac{1}{2})}^{2018}$ D、 ${(\frac{1}{2})}^{2019}$

查看试题解析
10. 如图，已知正方形ABCD的边长为4，P是对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接AP，EF.给出下列结论：①PD= $\sqrt{2}$ EC：②四边形PECF的周长为8；③△APD一定是等腰三角形：④AP=EF；⑤EF的最小值为 $2 \sqrt{2}$ ；⑥AP⊥EF.其中正确结论的序号为（）

A、①②④⑤⑥ B、①②④⑤ C、②④⑤ D、②④⑤⑥

查看试题解析

二、填空题

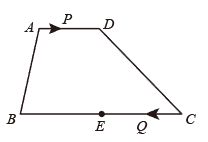
11. 若式子 $\sqrt{5 - x}$ 在实数范围内有意义，则 $x$ 的取值范围是

查看试题解析
12. 平面直角坐标系上有点A（﹣3，4），则它到坐标原点的距离为．

查看试题解析
13. 关于 $x$ 的方程 $m x^{2} - 2 x + 3 = 0$ 有两个不相等的实数根，那么 $m$ 的取值范围是．

查看试题解析
14. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ， $A D = 5$ ， $B C = 18$ ， E是 $B C$ 的中点．点P以每秒1个单位长度的速度从点A出发，沿 $A D$ 向点D运动；点Q同时以每秒3个单位长度的速度从点C出发，沿 $C B$ 向点B运动．点P停止运动时，点Q也随之停止运动，当运动时间t秒时，以点P，Q，E，D为顶点的四边形是平行四边形，则t的值为．

查看试题解析

三、解答题

15. 解方程： $3 x (2 x + 3) = 4 x + 6$

查看试题解析
16. 已知 $x = \sqrt{3} + \sqrt{2}$ ， $y = \sqrt{3} - \sqrt{2}$ ，求：

(1)、 $\frac{x}{y} + \frac{y}{x}$ 的值；

(2)、 $2 x^{2} + 6 x y + 2 y^{2}$ 的值．

查看试题解析
17. 如图，请在边长为1的小正方形组成的网格中画一个 $△ A B C$ ， $△ A B C$ 的三个顶点均在格点上，使它的三边长分别为 $\sqrt{5}$ ， $\sqrt{10}$ ， $\sqrt{13}$

查看试题解析
18. 如图所示， $▱ A B C D$ 的对角线 $A C$ 的垂直平分线与边 $A D$ ， $B C$ 分别相交于点E，F.求证：四边形 $A F C E$ 是菱形.

查看试题解析
19.
小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况．他从中随机调查了一定户数的家庭收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图．
分组
频数
百分比
600≤x＜800
2
5%
800≤x＜1000
6
15%
1000≤x＜1200
a
40%
1200≤x＜1400
9
22.5%
1400≤x＜1600
b
c
1600≤x＜1800
2
5%
合计
40
100%

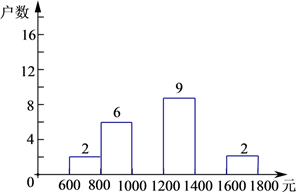
根据以上提供的信息，解答下列问题：

(1)、频数分布表中：a= ， b= ， c= ．

(2)、补全频数分布直方图．

(3)、请估计该居民小区家庭属于中等收入（大于1000不足1600元）的大约有多少户？

查看试题解析
20. 某商业街有店面房共195间，2016年平均每间店面房的年租金为10万元，由于物价上涨，到2018年平均每间店面房的年租金上涨到了12.1万元，据预测，当每间的年租金定为12.1万元时，可全部租出；若每间的年租金每增加1万元，就要少租出10间．该商业街管委会要为租出的商铺每间每年交各种费用1.1万元，未租出的商铺每间每年交各种费用5000元．

(1)、求2016年至2018年平均每间店面房年租金的平均增长率；

(2)、当每间店面房的年租金上涨多少万元时，该商业街的年收益（收益 $=$ 租金 $-$ 各种费用）为2305万元？

查看试题解析
21. 如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F、H在菱形ABCD的对角线BD上.

(1)、求证：BG=DE；

(2)、若E为AD中点，FH=2，求菱形ABCD的周长。

查看试题解析
22. 四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG

(1)、如图，求证：矩形DEFG是正方形；

(2)、若AB＝2 $\sqrt{2}$ ， CE＝2，求CG的长；

(3)、当线段DE与正方形ABCD的某条边的夹角是40°时，直接写出∠EFC的度数．

查看试题解析

分组	频数	百分比
600≤x＜800	2	5%
800≤x＜1000	6	15%
1000≤x＜1200	a	40%
1200≤x＜1400	9	22.5%
1400≤x＜1600	b	c
1600≤x＜1800	2	5%
合计	40	100%