安徽省合肥市庐江县2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-06-29 类型:期末考试
一、单选题
-
1. 要使 有意义,则x的取值范围为(( )A、x≤0 B、x≥1 C、x≥0 D、x≤12. 下面各点中,在函数y=﹣ x+3图象上的点是( )A、(3,0) B、(﹣2,2) C、(2,﹣2) D、(4,1)3. 某服装销售商在进行市场占有率的调查时,他最应该关注的是( )
A、服装型号的平均数 B、服装型号的众数 C、服装型号的中位数 D、最小的服装型号4. 下列计算正确的是( )A、 B、 C、 D、5. 四边形ABCD的对角线相交于点O,且 ,那么下列条件不能判断四边形ABCD为平行四边形的是( )A、 B、 C、 D、6. 一艘轮船和一艘快艇沿相同路线从甲港出发匀速行驶至乙港,行驶路程随时间变化的图象如图,则下列结论错误的是( ) A、轮船的速度为20千米时 B、轮船比快艇先出发2小时 C、快艇到达乙港用了6小时 D、快艇的速度为40千米时7. 如图,在平行四边形 中, 平分 ,则平行四边形 的周长是( )
A、轮船的速度为20千米时 B、轮船比快艇先出发2小时 C、快艇到达乙港用了6小时 D、快艇的速度为40千米时7. 如图,在平行四边形 中, 平分 ,则平行四边形 的周长是( ) A、16 B、18 C、20 D、248. 在△ABC中,AB=10,AC=2 ,BC边上的高AD=6,则另一边BC等于( )A、10 B、8 C、6或10 D、8或109. 已知一次函数 , 若y随着x的增大而增大,且它的图像与y轴交于负半轴,则直线的大致图像是( )A、
A、16 B、18 C、20 D、248. 在△ABC中,AB=10,AC=2 ,BC边上的高AD=6,则另一边BC等于( )A、10 B、8 C、6或10 D、8或109. 已知一次函数 , 若y随着x的增大而增大,且它的图像与y轴交于负半轴,则直线的大致图像是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )
10. 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )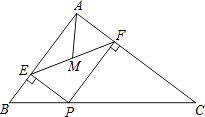 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 某商场为了招聘商品拆装上架员工一名,设置了计算机、语言和商品知识三项测试,并对这三项测试成绩按照2:3:5的比确定.若某应试者三项测试成绩分别为70,50,80,则该应试者的平均成绩是.12. 当 时,代数式 的值是 .13. 若一次函数y=kx+b(b为常数)的图象过点(3,4),且与y=x的图象平行,这个一次函数的解析式为 .14. 如图,在矩形中,对角线相交于点O,过点O作交于点已知的面积为3,连接则 , AE的长为 .
 15. 工人师傅做铝合金窗框分下面三个步骤进行:
15. 工人师傅做铝合金窗框分下面三个步骤进行:
⑴先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;⑵摆放成如图②的四边形,则这时窗框的形状是形,根据的数学原理是:;
⑶将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是形,根据的数学原理是: .
三、解答题
-
16. 计算:17. 有一架秋千,当它静止时,踏板离地的垂直高度DE=0.5m,将它往前推送2m(水平距离BC=2m)时,秋千的踏板离地的垂直高度BF=1.5m,秋千的绳索始终拉得很直,求绳索AD的长度
 18. 如图,在 中,点E在 的延长线上,点F在 的延长线上,满足 .连接 ,分别与 , 交于点 ,H.求证: .
18. 如图,在 中,点E在 的延长线上,点F在 的延长线上,满足 .连接 ,分别与 , 交于点 ,H.求证: . 19. 如图,在的方格纸中,是格点三角形(顶点在格点上),请按要求作图(注:只能用无刻度的直尺,且不能使用直尺的直角,并保留必要的作图痕迹).
19. 如图,在的方格纸中,是格点三角形(顶点在格点上),请按要求作图(注:只能用无刻度的直尺,且不能使用直尺的直角,并保留必要的作图痕迹). (1)、在图1中画出平行四边形 , 使得的面积与面积比为 .(2)、在图2中的上找一点F,画线段 , 使得将分成面积相等的两部分.20. 一次函数y=kx+b的图象经过A(1,6),B(−3,−2)两点.
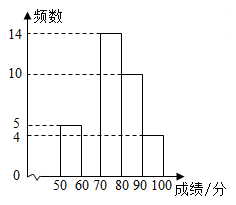
(1)、在图1中画出平行四边形 , 使得的面积与面积比为 .(2)、在图2中的上找一点F,画线段 , 使得将分成面积相等的两部分.20. 一次函数y=kx+b的图象经过A(1,6),B(−3,−2)两点. (1)、此一次函数的解析式;(2)、求△AOB的面积.21. 为加强同学们的疫情防控意识,某校开展了新型冠状病毒肺炎防护知识调研,现从全校学生的调研成绩中随机抽取名学生的调研成绩,并将他们的调研成绩(满分分)进行整理、描述和分析,数据分成五组: , , , , , 部分信息如下:①名学生的调研成绩频数分布直方图如图所示;
(1)、此一次函数的解析式;(2)、求△AOB的面积.21. 为加强同学们的疫情防控意识,某校开展了新型冠状病毒肺炎防护知识调研,现从全校学生的调研成绩中随机抽取名学生的调研成绩,并将他们的调研成绩(满分分)进行整理、描述和分析,数据分成五组: , , , , , 部分信息如下:①名学生的调研成绩频数分布直方图如图所示;②名学生的调研成绩在这一组的具体得分是 , , , , , , , , , , , , , ;
③名学生的调研成绩的平均数、中位数、众数(众数在这一组里)如下表.请根据所给信息,解答下列问题:
平均数
中位数
众数
a
b
(1)、表中a= , b= , 并补全频数分布直方图;(2)、从成绩在这一组的名学生中,随机抽出了名学生协助政教处普及疫情防控知识,这名学生的成绩分别为 , , , , , , 请计算这名学生成绩的方差;(3)、该校参加防护知识调研的学生共有人,学校计划让成绩排在前的学生获奖,请你说明最低分应该定为多少分?22. 快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:型号
甲
乙
每台每小时分拣快递件数(件)
1000
800
每台价格(万元)
5
3
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)、设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;(2)、购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?23. 如图正方形 , 点E、G、H分别在、、上,与相交于点O. (1)、如图1,当 ,
(1)、如图1,当 ,①求证:;
②平移图1中线段 , 使G点与D重合,H点在延长线上,连接 , 取中点P,连接 , 如图2,求证:;
(2)、如图3,当 , 边长 , , 则的长为(直接写出结果).