安徽省合肥市2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 关于x的方程 $(m - 2) x^{| m |} + m x - 1 = 0$ 是一元二次方程，则m值为（）

A、 $2$ 或 $- 2$ B、 $2$ C、 $- 2$ D、 $m \geq 0$ 且 $m \neq 2$

查看试题解析
2. 当 $2 x - 3 > 0$ 时，化简 $| 1 - x | + \sqrt{9 - 12 x + 4 x^{2}}$ 的结果是（）

A、x-2 B、 $2 - x$ C、 $3 x - 4$ D、 $4 - 3 x$

查看试题解析
3. 已知关于x的方程 $m x^{2} - (m + 2) x + 2 = 0$ 有两个不相等的正整数根，则m的值为（）

A、 $2$ B、 $1$ C、 $\frac{\sqrt{2} - 1}{3}$ D、 $2$ 或 $1$

查看试题解析
4. 如图， $▱ A B C D$ 中， $∠ A B C = 75 °$ ， $A F ⊥ B C$ 于F， $A F$ 交 $B D$ 于E，若 $D E = 2 A B$ ，则 $∠ A E D$ 的大小是（）

A、 $60 °$ B、 $65 °$ C、 $70 °$ D、 $75 °$

查看试题解析
5. 如图，点P是正方形 $A B C D$ 内一点， $P A = 1$ ， $P D = \sqrt{10}$ ， $∠ A P B = 135 °$ ，则 $P B$ 的长为（）

A、 $2 \sqrt{3}$ B、 $3 \sqrt{2}$ C、 $2 \sqrt{2}$ D、 $3 \sqrt{3}$

查看试题解析
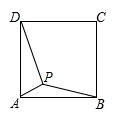6. 如图，点O为正六边形的中心，P，Q分别从点A（1，0）同时出发，沿正六边形按图示方向运动，点P的速度为每秒1个单位长度，点Q的速度为每秒2个单位长度，则第2020次相遇地点的坐标为（）

A、 $(- \frac{1}{2} ， \frac{\sqrt{3}}{2})$ B、 $(1 ， 0)$ C、 $(- \frac{1}{2} ， - \frac{\sqrt{3}}{2})$ D、 $(- 1 ， 0)$

查看试题解析
7. 如图，直线l上有三个正方形，若a，c的面积分别为5和11，则b的面积为（）

A、4 B、6 C、16 D、55

查看试题解析
8. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为 $5$ 里， $12$ 里， $13$ 里，则该沙田的面积为（）（“里”是我国市制长度单位， $1$ 里 $= 500$ 米）

A、 $7.5$ 平方千米 B、 $75$ 平方千米 C、 $1$ 平方千米 D、 $750$ 平方千米

查看试题解析
9. 如图，在正方形 $A B C D$ 中，点E、F分别是 $D C 、 A D$ 边上的动点，且 $A E ⊥ B F$ ，垂足为P，连接 $C P$ ．若正方形的边长为1，则线段 $C P$ 的最小值为（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{5} - 1}{2}$ D、 $\frac{\sqrt{5}}{4}$

查看试题解析
10. 如图，在△ABC中，∠ACB=90°，AC=BC=1，E、F为线段AB上两动点，且∠ECF=45°，过点E、F分别作BC、AC的垂线相交于点M，垂足分别为H、G.现有以下结论：①AB= $\sqrt{2}$ ；②AF+BE=EF；③当点E与点B重合时，MH= $\frac{1}{2}$ ；其中正确结论的个数是(　　)

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

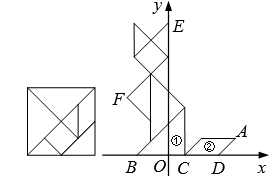
11. 已知关于x的一元二次方程 $k x^{2} + (2 k - 1) x + k + 2 = 0$ 的两个实数根一个大于1，一个小于1，则k的取值范围是．

查看试题解析
12. 如图，在平面直角坐标系中，有一只用七巧板拼成的“猫”，三角形①的边BC及四边形②的边CD都在x轴上，“猫”耳尖E在y轴上.若“猫”尾巴尖A的横坐标是1，则“猫”爪尖F的坐标是.

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ． D是 $A B$ 的中点，点E在直线 $B C$ 上运动，以 $D E$ 为边向左侧作正方形 $E D F G$ ，连接 $A F$ ，若 $A C = 3$ ，则 $A F$ 的最小值是．

查看试题解析
14. 阅读理解：对于任意正整数a，b，∵ ${(\sqrt{a} - \sqrt{b})}^{2} \geq 0$ ， ∴ $a - 2 \sqrt{a b} + b \geq 0$ ， ∴ $a + b \geq 2 \sqrt{a b}$ ，只有当 $a = b$ 时，等号成立；结论：在 $a + b \geq 2 \sqrt{a b}$ （a、b均为正实数）中，只有当 $a = b$ 时， $a + b$ 有最小值 $2 \sqrt{a b}$ .若 $m > 1$ ， $\sqrt{m} + \frac{1}{\sqrt{m} - 1}$ 有最小值为．

查看试题解析

三、解答题

15.

(1)、已知实数x，y满足 $x^{2} + 3 x + y - 5 = 0$ ，求 $x + y$ 的最大值；

(2)、已知a，b，c为正实数，且满足 $a^{2} + a c + a b - b^{2} = 0$ 和 $b^{2} + b a - c a - c^{2} = 0$ ，试判断以b，c， $a + b$ 为三边的长的三角形的形状，并说明理由．

查看试题解析
16. 如图，在四边形 $A B C D$ 中， $B C = C D$ ， $∠ C = 2 ∠ B A D$ . $O$ 是四边形 $A B C D$ 内一点，且 $O A = O B = O D$ .求证：

(1)、 $∠ B O D = ∠ C$ ；

(2)、四边形 $O B C D$ 是菱形.

查看试题解析
17. 我们把满足方程 $x^{2} + y^{2} + z^{2} = w^{2}$ 的正整数x，y，z，w称之为“三维勾股数”，如：① $1$ ， $2$ ， $2$ ， $3$ ；② $7$ ， $4$ ， $4$ ， $9$ ；③ $17$ ， $6$ ， $6$ ， $19$ ；④ $31$ ， $8$ ， $8$ ， $33$ ；…

(1)、已知x， $10$ ， $10$ ， y是“三维勾股数”，请求出x，y的值．

(2)、若u， $2 k$ ， $2 k$ ， v是三维勾股数（k为正整数），请直接用含k的式子分别表示u，v．

查看试题解析
18. 如图，在菱形 $A B C D$ 中， $∠ A B C = 60 °$ ， E为对角线 $A C$ 上一点，将线段 $D E$ 绕点D逆时针旋转 $60 °$ ，点E的对应点为F，连接 $B E$ ， $A F$ ， $C F$ ．

(1)、求证：B，C，F三点共线；

(2)、若点G为 $B E$ 的中点，连接 $A G$ ，求证： $A F = 2 A G$ ．

查看试题解析
19. 解方程 ${(x - 1)}^{2} - 5 (x - 1) + 4 = 0$ 时，我们可以将 $x - 1$ 看成一个整体，设 $x - 1 = y$ ，则原方程可化为 $y^{2} - 5 y + 4 = 0$ ，解得 $y_{1} = 1$ ， $y_{2} = 4$ ．当 $y = 1$ 时，即 $x - 1 = 1$ ，解得 $x = 2$ ；当 $y = 4$ 时，即 $x - 1 = 4$ ，解得 $x = 5$ ，所以原方程的解为 $x_{1} = 2$ ， $x_{2} = 5$ ．请利用这种方法求下列方程：

(1)、 ${(2 x + 5)}^{2} - (2 x + 5) - 2 = 0$ ；

(2)、 $3^{2 x} - 4 \times 3^{x} + 3 = 0$ ．

查看试题解析
20. 如图1，在正方形 $A B C D$ 内作 $∠ E A F = 45 °$ ， $A E$ 交 $B C$ 于点E， $A F$ 交 $C D$ 于点F，连接 $E F$ ，过点A作 $A H ⊥ E F$ ，垂足为H．如图2，将 $△ A D F$ 绕点A顺时针旋转 $90 °$ 得到 $△ A B G$ ．

(1)、求证： $△ A G E ≌ △ A F E$ ；

(2)、若 $B E = 2$ ， $D F = 3$ ，求 $A H$ 的长．

查看试题解析
21. “低碳生活，绿色出行”，2017年1月，某公司向深圳市场新投放共享单车640辆．

(1)、若1月份到4月份新投放单车数量的月平均增长率相同，3月份新投放共享单车1000辆．请问该公司4月份在深圳市新投放共享单车多少辆？

(2)、考虑到自行车市场需求不断增加，某商城准备用不超过70000元的资金再购进A，B两种规格的自行车100辆，已知A型的进价为500元/辆，售价为700元/辆，B型车进价为1000元/辆，售价为1300元/辆．假设所进车辆全部售完，为了使利润最大，该商城应如何进货？

查看试题解析
22. 定义：若关于x的一元二次方程 $a x^{2} + b x + c = 0$ $(a \neq 0)$ 的两个实数根为 $x_{1}$ ， $x_{2}$ $(x_{1} < x_{2})$ ，分别以 $x_{1}$ ， $x_{2}$ 为横坐标和纵坐标得到点 $M (x_{1} ， x_{2})$ ，则称点 $M$ 为该一元二次方程的衍生点．已知关于x的一元二次方程为 $x^{2} - 2 (m - 1) x + m^{2} - 2 m = 0$ ．

(1)、求证：不论m为何值，该方程总有两个不相等的实数根；

(2)、求衍生点M的轨迹的解析式；

(3)、若无论k $(k \neq 0)$ 为何值，关于x的方程 $a x^{2} + b x + c = 0$ 的衍生点M始终在直线 $y = k x - 2 (k - 2)$ 的图象上，求b与c满足的关系．

查看试题解析
23. 如图1， $∠ D A B$ 是 $▱ A B C D$ 的内角， $∠ D A B = 60 °$ ，

(1)、 $B F$ 平分 $∠ A B C$ ，交 $A D$ 于点F，过点A作 $A G / / B F$ ，过点F作 $F G / / A B$ ，判断四边形 $A B F G$ 的形状：；

(2)、旋转 $∠ D A B$ 到 $∠ F A E$ ，如图2，边 $A E$ 交 $B C$ 于点E，连接 $E F$ ， AE=AF．过点A作 $A G / / E F$ ，过点F作 $F G / / A E$ ．问： $B F$ 是否平分 $∠ A B C$ ．若是请证明，若不是请说明理由．

(3)、四边形 $A E F G$ 在（2）的条件下，若恰好 $E G / / A B$ ，如图3．连接 $D G$ 并延长，交 $B A$ 的延长线于点H．求证： $B C = 3 A B$ ．

查看试题解析