安徽省滁州市来安县2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-06-29 类型:期末考试
一、单选题
-
1. 若在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是( )A、5 B、4 C、7 D、63. 下列计算正确的是( )A、 B、 C、 D、4. 如图,在▱ABCD中,对角线AC、BD相交于点O,若再添加一个条件使▱ABCD成为矩形,则该条件不可以是( )
 A、AC=BD B、AO=BO C、∠BAD=90° D、∠AOB=90°5. 为执行“均衡教育”政策,某县2019年投入教育经费2650万元,预计到2021年底三年累计投入1.2亿元.若每年投入教育经费的年平均增长率为x,则下列方程正确的是( )A、 B、 C、 D、6. 若关于x的一元二次方程mx2+2mx+4=0有两个相等的实数根,则m的值为( )A、0 B、4 C、0或4 D、0或﹣47. 在ABC中,三边长分别为a,b,c,且 , , 则ABC是( )A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形8. 如图,已知E是正方形ABCD对角线AC上一点,且AB=AE,则∠DBE度数是( )
A、AC=BD B、AO=BO C、∠BAD=90° D、∠AOB=90°5. 为执行“均衡教育”政策,某县2019年投入教育经费2650万元,预计到2021年底三年累计投入1.2亿元.若每年投入教育经费的年平均增长率为x,则下列方程正确的是( )A、 B、 C、 D、6. 若关于x的一元二次方程mx2+2mx+4=0有两个相等的实数根,则m的值为( )A、0 B、4 C、0或4 D、0或﹣47. 在ABC中,三边长分别为a,b,c,且 , , 则ABC是( )A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形8. 如图,已知E是正方形ABCD对角线AC上一点,且AB=AE,则∠DBE度数是( ) A、15° B、32.5° C、22.5° D、30°9. 某公司为了解职工参加体育锻炼情况,对职工某一周平均每天锻炼(跑步或快走)的里程进行统计(保留整数),并将他们平均每天锻炼的里程数据绘制成扇形统计图,关于他们平均每天锻炼里程数据,下列说法错误的是( )
A、15° B、32.5° C、22.5° D、30°9. 某公司为了解职工参加体育锻炼情况,对职工某一周平均每天锻炼(跑步或快走)的里程进行统计(保留整数),并将他们平均每天锻炼的里程数据绘制成扇形统计图,关于他们平均每天锻炼里程数据,下列说法错误的是( ) A、平均每天锻炼里程数据的中位数是2 B、平均每天锻炼里程数据的众数是2 C、平均每天锻炼里程数据的平均数是2.34 D、平均每天锻炼里程数不少于4km的人数占调查职工的20%10. 如图,在RtABC中, , , , 两顶点A,B分别在平面直角坐标系的y轴,x轴的正半轴上滑动,点C在第一象限内,连接OC,则OC的长的最大值为( )
A、平均每天锻炼里程数据的中位数是2 B、平均每天锻炼里程数据的众数是2 C、平均每天锻炼里程数据的平均数是2.34 D、平均每天锻炼里程数不少于4km的人数占调查职工的20%10. 如图,在RtABC中, , , , 两顶点A,B分别在平面直角坐标系的y轴,x轴的正半轴上滑动,点C在第一象限内,连接OC,则OC的长的最大值为( ) A、16 B、18 C、 D、
A、16 B、18 C、 D、二、填空题
-
11. 若最简二次根式与是同类二次根式,则x的值为12. 下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差S2:
甲
乙
丙
丁
平均数x(cm)
175
173
175
174
方差S2(cm2)
3.5
3.5
12.5
15
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择 .
13. 若a是方程的解,则代数式的值为.14. 已知正方形ABCD中,AB=3,P为边CD上一点,DP=1,Q为边BC上一点,若△APQ为等腰三角形,则CQ的长为 .
三、解答题
-
15. 计算: .16. 解方程:2x2﹣3x=5.17. 如图,在正方形网格中每个小正方形的边长为1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形:

( 1 )在图(1)网格中画出长为的线段AB.
( 2 )在图(2)网格中画出一个腰长为 , 面积为3的等腰
18. 已知关于x的一元二次方程x2﹣mx﹣2=0.(1)、求证:无论m取何实数,该方程总有两个不相等的实数根;(2)、若方程的一个根为2,求m的值及另一个根.19. 如图,在ABC中,D,E,F分别是AB,BC,AC的中点,连接DF,EF,BF. (1)、求证:四边形BEFD是平行四边形;(2)、若 , , 求四边形BEFD的周长20. 某公司设计了一款工艺品,每件的成本是40元,为了合力定价,投放市场进行试销:据市场调查,销售单价是50元时,每天的销售量是100件,而销售单价每提高1元,每天就减少售出2件,但要求销售单价不得超过65元.(1)、若销售单价为每件60元,求每天的销售利润;(2)、要使每天销售这种工艺品盈利1350元,那么每件工艺品售价应为多少元?21. 如图,平行四边形ABCD中,AE=CE.
(1)、求证:四边形BEFD是平行四边形;(2)、若 , , 求四边形BEFD的周长20. 某公司设计了一款工艺品,每件的成本是40元,为了合力定价,投放市场进行试销:据市场调查,销售单价是50元时,每天的销售量是100件,而销售单价每提高1元,每天就减少售出2件,但要求销售单价不得超过65元.(1)、若销售单价为每件60元,求每天的销售利润;(2)、要使每天销售这种工艺品盈利1350元,那么每件工艺品售价应为多少元?21. 如图,平行四边形ABCD中,AE=CE. (1)、用尺规或只用无刻度的直尺作出∠AEC的角平分线,保留作图痕迹,不需要写作法.(2)、设∠AEC的角平分线交边AD于点F,连接CF,求证:四边形AECF为菱形.22. 中华文明,源远流长;中华汉字,寓意深广,某校举办了以“感悟汉字深厚底蕴,弘扬中华传统文化”为主题的汉字听写大赛,全校3600名学生都参加了此次大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
(1)、用尺规或只用无刻度的直尺作出∠AEC的角平分线,保留作图痕迹,不需要写作法.(2)、设∠AEC的角平分线交边AD于点F,连接CF,求证:四边形AECF为菱形.22. 中华文明,源远流长;中华汉字,寓意深广,某校举办了以“感悟汉字深厚底蕴,弘扬中华传统文化”为主题的汉字听写大赛,全校3600名学生都参加了此次大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:成绩x/分
50≤x<60
60≤x<70
70≤x<80
80≤x<90
90≤x≤100
频数
10
30
40
m
50
频率
0.05
0.15
n
0.35
0.25
 (1)、m=;n=;(2)、请补全频数分布直方图;(3)、这次比赛成绩的中位数会落在分数段;(4)、若成绩在90分以上(包括90分)的为“优”等,估计该校参加这次比赛的3600名学生中成绩“优”等约有多少人?23. 如图1,正方形中,点E是延长线上一点,连接 , 过点B作于点F,交于点G.
(1)、m=;n=;(2)、请补全频数分布直方图;(3)、这次比赛成绩的中位数会落在分数段;(4)、若成绩在90分以上(包括90分)的为“优”等,估计该校参加这次比赛的3600名学生中成绩“优”等约有多少人?23. 如图1,正方形中,点E是延长线上一点,连接 , 过点B作于点F,交于点G.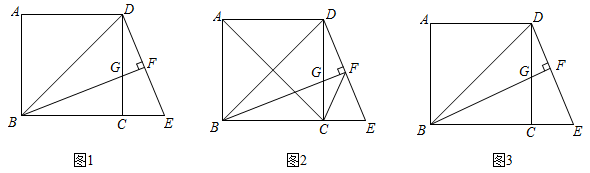 (1)、求证: .(2)、如图2,连接、 . 若平分 , 求证:平分 .(3)、如图3,若G为中点, , 求的长.
(1)、求证: .(2)、如图2,连接、 . 若平分 , 求证:平分 .(3)、如图3,若G为中点, , 求的长.