安徽省安庆市太湖县2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中，一定是二次根式的是（　　）

A、 $\sqrt{x}$ B、 $\sqrt{x + 2}$ C、 $\sqrt{x^{2} + 2}$ D、 $\sqrt{- x}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{6} \div \sqrt{3} = \sqrt{2}$ B、 $\sqrt{{(- 3)}^{2}} = - 3$ C、 $- {(\sqrt{3})}^{2} = 3$ D、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$

查看试题解析
3. 下列运算正确的是（）

A、 ${(3 \sqrt{2})}^{2} = 6$ B、 $\sqrt{{(\sqrt{3} - 2)}^{2}} = 2 - \sqrt{3}$ C、 ${(\sqrt{3} - \sqrt{2})}^{2} = 3 - 2$ D、 $(4 + 2 \sqrt{3}) (4 - 2 \sqrt{3}) = 10$

查看试题解析
4. 下列二次根式中，与 $\sqrt{2}$ 是同类二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{8}$ C、 $\sqrt{12}$ D、 $\sqrt{20}$

查看试题解析
5. 下列二次根式中，最简二次根式是（　　）

A、 $\sqrt{7}$ B、 $\sqrt{9}$ C、 $\sqrt{12}$ D、 $\sqrt{\frac{2}{3}}$

查看试题解析
6. 当 $a + b = 4$ 时，关于x的一元二次方程 $- a x^{2} + b x + 2 = 0$ 的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
7. 随着我国新能源汽车的生产技术不断提升，市场上某款新能源汽车的价格由今年3月份的270000元/辆下降到5月份的243000元/辆．若价格继续下降，且月平均降价的百分率保持不变，则预测到今年7月份该款新能源汽车的价格将会（）．（参考数据： $\sqrt{0.9} \approx 0.95$ ）

A、低于22万元/辆 B、低于 $21.5$ 万元/辆 C、超过22万元/辆 D、超过23万元/辆

查看试题解析
8. 小玲的爸爸在钉制平行四边形框架时，采用了一种方法：如图所示，将两根木条AC，BD的中点重叠，并用钉子固定，则四边形ABCD就是平行四边形，这种方法的依据是（）

A、对角线互相平分的四边形是平行四边形 B、两组对角分别相等的四边形是平行四边形 C、两组对边分别相等的四边形是平行四边形 D、两组对边分别平行的四边形是平行四边形

查看试题解析
9. 定义；如果一元二次方程 $a x^{2} + b x + c = 0$ (a≠0)满足a+b+c=0，那么我们称这个方程为“蜻蜓”方程.已知关于x的方程 $a x^{2} + b x + c = 0$ (a≠0)是“蜻蜓”方程，且有两个相等的实数根，则下列结论中正确的是（）

A、a=c≠b B、a=b≠c C、b=c≠a D、a=b=c

查看试题解析
10. 如图，在矩形ABCD中，AB=3，对角线AC，BD相交于点O，M为AO的中点， $M E / / A B$ 交OB于E， $M F / / O D$ 交AD于F，若 $M E = M F$ ，则EF的值为（）

A、3 B、 $\sqrt{3}$ C、 $\frac{3 \sqrt{3}}{2}$ D、4

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{x + 2021}$ 有意义，则x的取值范围是．

查看试题解析
12. 一元二次方程 $2 x^{2} + 6 x = - 5$ 化成一般式为．

查看试题解析
13. 在直角三角形中，两边长分别为6、8，则第三条边长．

查看试题解析
14. 如图，在长方形ABCD中，E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG交CD于点F，连接EF，若AB＝6，BC＝4 $\sqrt{6}$ ，则

(1)、∠BEF＝；

(2)、DF＝．

查看试题解析

三、解答题

15. 解方程：x²+4x﹣1=0．

查看试题解析
16. $\sqrt{48} \div \sqrt{3} - 2 \sqrt{\frac{1}{5}} \times \sqrt{10} + \sqrt{8}$ ．

查看试题解析
17. 一架梯子AB长25米，如图斜靠在一面墙上，梯子底端B离墙7米．

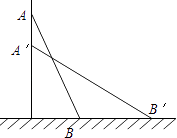(1)、这个梯子的顶端距地面有多高？

(2)、如果梯子的顶端下滑了4米，那么梯子底部在水平方向滑动了4米吗？为什么？

查看试题解析
18. 如图，正方形网格中，每个小方格的边长为1，请完成：

(1)、从A点出发画线段AB、AC并连接BC，使AB＝ $\sqrt{5}$ ， AC＝ $2 \sqrt{2}$ ， BC＝ $\sqrt{17}$ ，且使B、C两点也在格点上；

(2)、比较两个数 $\sqrt{5}$ 和 $2 \sqrt{2}$ 的大小；

(3)、请求出图中△ABC的面积．

查看试题解析
19. 目前，以5G为代表的战略性新兴产业蓬勃发展．某市2019年开始拥有5G用户，年底有5G用户2万户，计划到2021年底5G用户数累计达到8.72万户．求这两年全市5G用户数的年平均增长率．（参考数据： $\sqrt{14.44} = 3.8$ ， $\sqrt{4.36} ≌ 2.09$ ）

查看试题解析
20. 如图，矩形ABCD的对角线相交于点O，F是矩形ABCD上方一点，连接CF交BD于点E，且E是CF的中点，连接AF，DF， $D F / / A C$ ．

(1)、求证：四边形AODF是菱形；

(2)、若 $∠ A O B = 60 °$ ， $∠ A F C = 90 °$ ， $A B = 2$ ，求CF的长．

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} + 2 x + 2 k - 4 = 0$ 有两个不相等的实数根．

(1)、求k的取值范围；

(2)、若k为正整数，且该方程的两个根都是整数，求k的值并求出方程的两个整数根．

查看试题解析
22. 2021年4月29日11时许，我国“天和”核心舱用长征五号B遥二运载火箭在海南文昌发射成功，正式拉开我中国空间站建造的序幕，为了解我校初三学生对我国空间站建设的关注程度，随机抽取了男、女学生若干名（抽取的男女生人数相同）进行问卷测试，问卷共30道选择题（每题1分，满分30分），现将得分情况统计，并绘制了如下不完整的统计图：（数据分组为A组： $x < 18$ ， B组： $18 \leq x < 22$ ， C组： $22 \leq x < 26$ ， D组： $26 \leq x \leq 30$ ， x表示问卷测试的分数），其中男生得分处于C组的有14人．
男生C组得分情况分别为：22，23，24，22，23，24，25，22，24，25，23，22，25，22；男生、女生得分的平均数、中位数、众数（单位：分）如表所示：
组别
平均数
中位数
众数
男
20
a
22
女
20
23
20

(1)、随机抽取的男生人数为人，表格中a的值为，补全条形统计图：

(2)、通过以上数据分析，你认为是男生的成绩好还是女生的成绩好？说明理由（一条理由即可）

(3)、如果我校男生、女生各1400人，那么估计此次参加问卷测试成绩不低于26分的人数有多少人？

查看试题解析
23. 问题情境：
在数学课外小组活动中，老师要求大家对“菱形的剪拼”问题进行探究．
如图1，将边长为4， $∠ A = 45$ 度的菱形纸片ABCD沿着对角线BD剪开，得到 $△ A B D$ 和 $△ B^{'} D C$ ．将 $△ B^{'} D C$ 绕着点D逆时针旋转．

(1)、初步探究：
“爱心小组”将 $△ B^{'} D C$ 绕点D逆时针旋转，当 $D B^{'} / / A B$ 时， $∠ B D B^{'}$ 的度数为；

(2)、再次探究：
“勤奋小组”将 $△ B^{'} D C$ 绕点D逆时针旋转至图2，连接AC， $B B^{'}$ ，此时四边形 $A B B^{'} C$ 是矩形，求 $∠ B D B^{'}$ 的度数；

(3)、深入探究：
“创新小组”将 $△ B^{'} D C$ 绕点D逆时针旋转至图3，此时点B，D， $B^{'}$ 恰好在一条直线上，延长BA， $B^{'} C$ 交于点E，试判断四边形ADCE的形状，并说明理由．

查看试题解析

组别	平均数	中位数	众数
男	20	a	22
女	20	23	20