安徽省安庆市怀宁县2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，能与 $\sqrt{3}$ 合并的是（　　）

A、 $\sqrt{0.3}$ B、 $\sqrt{\frac{2}{3}}$ C、 $\sqrt{12}$ D、 $\sqrt{18}$

查看试题解析
2. 已知一正多边形的内角与其相邻的外角的比为3：1，则该多边形的边数为（　　）

A、6 B、8 C、9 D、10

查看试题解析
3. 了解时事新闻，关心国家重大事件是每个中学生应具备的素养，在学校举行的新闻事件比赛中，知道“祝融号”成功到达火星的同学有40人，频率为0.8，则参加比赛的同学共有（　　）

A、32人 B、40人 C、48人 D、50人

查看试题解析
4. 在△ABC中以下条件不能判定△ABC是直角三角形的个数有（　　）个：
条件①：∠A=∠C-∠B；
条件②：三角形三边a，b，c的比3：4：5；
条件③：∠A：∠B：∠C=3：4：5；
条件④：a=5、b=12、c=13．

A、1 B、2 C、3 D、0

查看试题解析
5. 关于x的一元二次方程x²﹣（2m﹣1）x﹣m﹣2＝0实数根的情况最确切的是（　　）

A、有实数根 B、无实根 C、有两个相等实根 D、有两个不相等的实根

查看试题解析
6. 如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB＝5，AD＝12，则四边形ABOM的周长为（　　）

A、18 B、20 C、21 D、24

查看试题解析
7. 远离白色垃圾从我做起，小明统计了上周一至周日7天他家使用塑料袋个数分别为：11，10，11，13，11，13，15关于这组数据，小明得出如下结果，其中错误的是（　　）

A、众数是11 B、平均数是12 C、方差是 $\frac{18}{7}$ D、中位数是13

查看试题解析
8. 四边形不具有稳定性，如图，矩形ABCD当改变内角大小就变成平行四边形ABC'D'，若∠D'AB=30°，则平行四边形ABC'D'的面积与矩形ABCD的面积之比是（　　）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、1

查看试题解析
9. 如图，某小区有一矩形ABCD空地，AB=8，BC=6，现设计成五块，其中正方形AEFG与正方形CIJK全等，矩形DGHI与矩形BKLE全等，中间为矩形LJHF，当矩形LJHF面积等于1时，设AE长为x，则x的值为（　　）

A、3 B、3.2 C、3.5 D、3.6

查看试题解析
10. 如图，菱形ABCD的边长为2，且∠DAB＝60°，E是BC的中点，P为BD上一点且△PCE的周长最小，则△PCE的周长的最小值为（　　）

A、 $\sqrt{3} + 1$ B、 $\sqrt{7} + 1$ C、 $2 \sqrt{3} + 1$ D、 $2 \sqrt{7} + 1$

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{2 x - 1}$ 在实数范围内有意义，则 $x$ 的取值范围是.

查看试题解析
12. 已知一组数据a、b、c、d、e的方差为1.2，则新的数据2a﹣1、2b﹣1、2c﹣1、2d﹣1、2e﹣1的方差是．

查看试题解析
13. 如图，正方形ABCD的边长为4，E是BC延长线上一点，P是∠DCE平分线上任意一点则△PBD的面积是．

查看试题解析
14. 如图，在矩形ABCD中，点E、F分别在AD、BC上，将△ABE沿BE翻折，使点A落在对角线BD上的M点，将△CDF沿DF翻折，使点C落在对角线BD上的N点．

(1)、四边形BFDE的形状是．

(2)、若四边形BFDE是菱形，BE=4，则菱形BFDE的面积为．

查看试题解析

三、解答题

15. 计算： $(\sqrt{3} + 1) (\sqrt{3} - 1) + \sqrt{8} - \sqrt{\frac{9}{2}}$ ．

查看试题解析
16. 解方程：x²﹣4x+1=0

查看试题解析
17. 在某段公路的正上方有一摄像头A距离地面7米，一天李叔叔驾驶的汽车正沿公路笔直匀速驶来，当行驶到B点时第一次摄像，此时AB两点相距25米，1.5秒后第二次摄像汽车恰好行驶到A点正下方C点，已知该路段限速60km/h，请判断李叔叔是否超速，说明理由．

查看试题解析
18. 已知关于x的方程ax²+2x﹣3＝0有两个不相等的实数根．

(1)、求a的取值范围；

(2)、若此方程的一个实数根为1，求a的值及方程的另一个实数根．

查看试题解析
19. 如图，在正方形网格中，每个小正方形的边长为1．

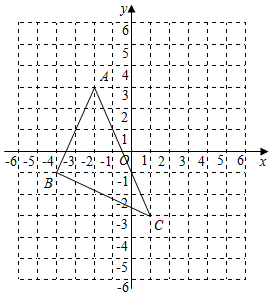(1)、在图中画出以AC为对角线的平行四边形ABCD；

(2)、写出D的坐标和平行四边形ABCD的面积．

查看试题解析
20. “独秀故里、黄梅之乡、长诗圣地”的怀宁誉满华夏，如今蓝莓已悄然成我县新的名片，在产业政策的积极引导和果农科学管理下，我县今年蓝莓可采摘面积和每亩平均产量都较去年有所增加，经调查可采摘面积的增长率是每亩平均产量增长率的2倍，使得我县今年蓝莓总产量比去年多15.5%，求今年每亩平均产量的增长率．（提示32²＝1024）

查看试题解析

21. 2021年5月22日，共和国勋章奖获得者、被誉为“杂交水稻之父”的袁隆平爷爷因病逝世，为深切缅怀纪念袁隆平爷爷，某校主办了以“热爱劳动，珍惜粮食”为主题的大赛，全校2500名学生都参加了此次大赛，赛后发现所有参赛学生的成绩均不低于50分，为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：

成绩x/分	50≤x＜60	60≤x＜70	70≤x＜80	80≤x＜90	90≤x＜100
频数	10	30	40	m	50
频率	0.05	0.15	n	0.35	0.25

(1)、n＝；

(2)、请补全频数分布直方图；

(3)、这次比赛成绩的中位数会落在分数段；（简要说明理由）

(4)、若成绩在90分以上（包括90分）的为“优”等，估计该校参加这次比赛的2500名学生中成绩“优”等约有多少人？

查看试题解析

22. 如图在正方形ABCD中，点F在CD延长线上，点E在BC边上，且BE=DF，连接EF交对线BD与点G，连接AE，AF，AG．

(1)、求证：AE=AF．

(2)、求证：BG-DG= $\sqrt{2}$ DF．

(3)、若DG=4，DF= $\sqrt{2}$ ，直接写出正方形ABCD的边长= ．

查看试题解析