云南省玉溪市红塔区2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 第七次全国人口普查结果公布的数据显示，全国人口共141178万人，其中具有大学文化程度的人口为218360000人，将218360000用科学记数法可表示为（）

A、141780×10⁹ B、2.1836×10⁹ C、21.836×10⁸ D、2.1836×10⁸

查看试题解析
2. 如图，直线a，b与射线c相交于同一点，c⊥a，若∠1＝35°，则∠2的度数为（）

A、35° B、45° C、55° D、65°

查看试题解析
3. 下列采用的调查方式中，不合适的是（）

A、了解某班学生的身高情况，采用全面调查 B、检测抚仙湖水的水质，采用全面调查 C、调查云南省中学生的手机使用时间，采用抽样调查 D、考核某市创建全国文明城市的情况，采用抽样调查

查看试题解析
4. 若x＜y，则下列不等式一定成立的是（）

A、﹣2x＞﹣2y B、 $\frac{x}{3} > \frac{y}{3}$ C、x+1＞y+1 D、1﹣x＜1﹣y

查看试题解析
5. 如图，点A，B，E在同一条直线上，不能判定AD $/ /$ BC的条件是（）

A、∠A＝∠CBE B、∠C+∠D＝180° C、∠C＝∠CBE D、∠A+∠ABC＝180°

查看试题解析
6. 在平面直角坐标系的第四象限内有一点P，点P到x轴的距离为7，到y轴的距离为8，则点P的坐标是（）

A、（﹣8，7） B、（8，﹣7） C、（7，﹣8） D、（8，﹣7）或（8，7）

查看试题解析
7. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有堆、兔同笼，上有三十五头下有九十四足．问雉、兔各几何？”意思是：一个笼中装有鸡和兔子，上面数共有35个头，下面数共有94只脚，问鸡和兔各有几只？设有x只兔子，y只鸡，则可列方程组为（）

A、 ${\begin{array}{l} x + y = 35 \\ 4 x + 2 y = 94 \end{array}$ B、 ${\begin{array}{l} x + y = 94 \\ 2 x + 4 y = 35 \end{array}$ C、 ${\begin{array}{l} x + y = 94 \\ 4 x + 2 y = 94 \end{array}$ D、 ${\begin{array}{l} x + y = 94 \\ 2 x + 4 y = 35 \end{array}$

查看试题解析
8. 若关于x的不等式组 ${\begin{array}{l} x - a ＞ 1 \\ 4 - 2 x \leq 0 \end{array}$ 的解集为x≥2，则a的取值范围为（）

A、a＜2 B、a＞1 C、a≤1 D、a＜1

查看试题解析

二、填空题

9. 若实数a的相反数是| $- \sqrt{2}$ |，则a的值为．

查看试题解析
10. 如图，AB $/ /$ CD，∠2＝135°，则∠1的度数是．

查看试题解析
11. 下列各数 $\sqrt{9}$ ， $\frac{11}{7}$ ， $\sqrt[3]{4}$ ， 3.1415，﹣2021，2π，0131131113…（每相邻两个3之间依次多1个1）中，无理数的个数有个．

查看试题解析
12. 若x，y满足方程组 ${\begin{array}{l} x + 7 y = 4 \\ 2 x - 3 y = 2 \end{array}$ ，则3x+4y的值为．

查看试题解析
13. 按一定规律排列的单项式：a，﹣2a，4a，﹣8a，16a，﹣32a，64a，…，第2021个单项式是．

查看试题解析
14. 已知点O、A、B在同一条直线上，点C是线段OA的中点，点D是线段OB的中点，若线段OA＝25cm，线段OB＝15cm，则线段CD的长度为．

查看试题解析

三、解答题

15. 计算：（﹣1）²⁰²⁰﹣（﹣2）²+ $\sqrt{4} + \sqrt[3]{- 27}$ ．

查看试题解析
16. 解方程：

(1)、2x²﹣50＝0；

(2)、 $1 - \frac{6 - 2 x}{3} = \frac{x - 1}{2}$ ．

查看试题解析
17. 解不等式组： ${\begin{array}{l} 2 x - 5 \leq 1 \\ 3 x + 2 (1 - 2 x) ＜ 4 \end{array}$ ，并将解集在数轴上表示出来．

查看试题解析
18. 根据条件进行推理，在横线上补全证明过程及推理依据．
如图，已知：∠B+∠BDE＝180°，∠ADE＝∠EFC，求证：∠A＝∠FEC．
证明：∵∠B+∠BDE＝180°，
∴DE∥BC（    ）．
∴∠EFC＝  ▲  （两直线平行，内错角相等）．
∵∠ADE＝∠EFC（已知），
∴∠ADE＝  ▲  （等量代换），
∴AB∥EF（     ）．
∴∠A＝∠FEC（    ）．

查看试题解析
19. 睡眠是机体复原整合和巩固记忆的重要环节，对促进中小学生大脑发育、骨骼生长、视力保护、身心健康和提高学习能力与效率至关重要.2021年3月，教育部办公厅印发了《关于进一步加强中小学生睡眠管理工作的通知》，文件明确了学生睡眠时间的要求，初中生每天睡眠时间应达到9小时．某初中学校为了解学生每天的睡眠时间t（单位：小时），在全校1000名学生中随机抽取部分学生进行了一次问卷调查，并将调查结果分为6≤t＜7、7≤t＜8、8≤t＜9、9≤t＜10四个组进行统计，根据统计的信息，绘制了如图不完整的频数分布直方图、扇形统计图．根据以上信息，解答下列问题：

(1)、填空：本次调查中，样本容量为，睡眠时间在6≤t＜7范围内的学生有人，占抽取学生的百分比为；在扇形统计图中，8≤t＜9对应的圆心角∠1的度数是度；

(2)、若睡眠时间未达到9小时的学生需要加强睡眠管理，则该校全校学生需要加强睡眠管理的学生大约有多少人？

查看试题解析
20. 如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（﹣2，1）、B（﹣3，﹣2）、C（﹣1，﹣1），若把△ABC向右平移5个单位长度，再向上平移3个单位长度得到△A′B′C′，点A、B、C的对应点分别为A′，B′，C′．

(1)、写出A′，B′，C′的坐标；

(2)、在图中画出平移后的△A′B′C′；

(3)、求△A′B′C′的面积．

查看试题解析
21. 某数学兴趣小组探究命题“两边分别平行的两个角相等”是否是真命题，甲同学认为该命题是真命题，并作图如图1所示，已知AB∥DE，AC∥DF，AC与DE交于点G．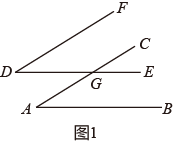

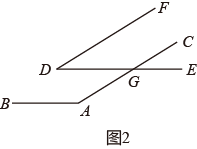(1)、根据甲同学的作图及题设，求证：∠A＝∠D；

(2)、乙同学对甲同学的判断提出质疑，认为该命题不一定成立，是假命题，并作图如图2所示，题设与甲同学相同，得到∠A≠∠D，根据乙同学的作图，试判断∠A与∠D的数量关系，并说明理由．

查看试题解析
22. 玉溪是滇中革命的摇篮，是国歌曲作者聂耳的故乡，聂耳是玉溪的骄傲，是伟大的人民音乐家，他短暂的一生为我们留下了37首脍炙人口的革命歌曲，用热血音符唤起了民族精神．为大力弘扬聂耳精神，传承红色文化，赓续红色血脉，在庆祝中国共产党成立100周年之际，某校计划组织226名师生到聂耳文化广场参加以“弘扬聂耳精神，唱响时代旋律”为主题的“聂耳和国歌的故事”红色学习体验活动，经过研究，决定租用一共10辆A、B两种型号的客车作为交通工具，已知1辆A型号客车与2辆B型号客车一共可载客50人，2辆A型号客车与3辆B型号客车一共可载客90人．

(1)、1辆A型号客车和1辆B型号客车分别可载客多少人？

(2)、若参加活动的师生都乘坐这两种型号的客车，且所有客车不允许超载，则至少需要租用几辆A型号客车？

查看试题解析
23. 如图，在点O为原点的平面直角坐标系中，点A在x轴上，且点A的横坐标的值等于16的算术平方根．将线段OA先向左平移1个单位长度，再向上平移2个单位长度，得到线段BC，点O、A的对应点分别为点B、C，BC与y轴交于点D，连接OB，AC，点P是线段AC上的一个动点，连接PO，PD．

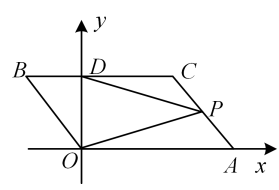(1)、直接写出点A、B、C的坐标；

(2)、当点P在AC上移动时（不与点A，C重合）， $\frac{∠ C D P + ∠ A O P}{∠ D P O}$ 的值是否是定值？若是，直接写出这个定值；若不是，请说明理由；

(3)、在直线BC上是否存在一点Q，使得△QBO的面积等于四边形OACB面积的 $\frac{1}{8}$ ，若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析