云南省曲靖市2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 16的算术平方根是（）

A、 $\pm 4$ B、 $- 4$ C、4 D、 $\pm 8$

查看试题解析
2. 坐标平面内下列各点中，在x轴上的点是（）

A、（0，3） B、（﹣3，0） C、（﹣1，2） D、（﹣2，﹣3）

查看试题解析
3. 为了了解某县七年级9800名学生的视力情况，从中抽查了100名学生的视力，就这个问题来说，下列说法正确的是（）

A、9800名学生是总体 B、每个学生是个体 C、100名学生是所抽取的一个样本 D、样本容量是100

查看试题解析
4. 二元一次方程2x+y=5的正整数解有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 若x＞y，则下列式子错误的是（）

A、x﹣2＞y﹣2 B、﹣3x＞﹣3y C、x+4＞y+4 D、 $\frac{x}{3} > \frac{y}{3}$

查看试题解析
6. 在﹣2， $\sqrt{4}$ ， $\sqrt{2}$ ， 3.14， $\sqrt[3]{- 27}$ ， $\frac{22}{7}$ ， 2.010010001…（每两个1之间0的个数逐渐增加1个），这7个数中，无理数共有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
7. 如图，点E在AD的延长线上，下列条件中能判断BC∥AD的是（）

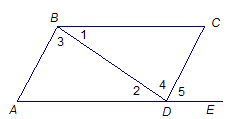A、∠3=∠4 B、∠A+∠ADC=180° C、∠1=∠2 D、∠A＝∠5

查看试题解析
8. 在下列各式中，计算正确的是（）

A、a²+a³＝a⁵ B、 $\sqrt{9}$ ＝±3 C、 $\sqrt{{(- 6)}^{2}}$ ＝﹣6 D、3 $\sqrt{2}$ ﹣ $\sqrt{2}$ ＝2 $\sqrt{2}$

查看试题解析

二、填空题

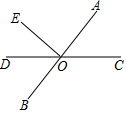
9. 不等式 $\frac{x - 1}{3} - \frac{3 x + 4}{6} > - 2$ 的解集是．

查看试题解析
10. 如图，直线AB和CD交于点O，EO⊥AB，垂足为O，∠AOD＝125°，则∠COE＝°．

查看试题解析
11. 将一块直角三角板的直角顶点放在长方形直尺的一边上，如 $∠ 1 = 4 3^{∘}$ ，那么∠ $2$ 的度数为

查看试题解析
12. 不等式了 $\frac{1}{3} (x - m) > 3 - m$ 的解集为 $x > 5$ ，则 $m$ 的值为.

查看试题解析
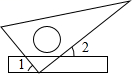13. 已知x²＝3，那么在数轴上与实数x对应的点可能是．

查看试题解析
14. 下列图形都是由同样大小的圆点按照一定规律所组成的，其中第一个图形中一共有3个圆点，第二个图形中一共有8个圆点，第三个图形中一共有15个圆点，…，按此规律排列下去，第10个图形中圆点的个数为．

查看试题解析

三、解答题

15. 计算：﹣2²× $\sqrt{\frac{1}{4}}$ ﹣ $\sqrt[3]{8} + \sqrt{9}$ ×（﹣1）²⁰²¹ ．

查看试题解析
16. 二元一次方程组 ${\begin{array}{l} x - 2 y = - 3 \\ 3 x + y = 5 \end{array}$ 的解满足 $2 x - k y = 1$ ，求k的值．

查看试题解析
17. 解不等式组 ${\begin{array}{l} \frac{2 x + 1}{3} - 1 < \frac{3 x + 2}{2} \\ 5 x \geq 6 x - 3 \end{array}$ ，并将其解集在数轴上表示出来．

查看试题解析
18. 如图，AD∥BC，AD平分∠EAC，你能确定∠B与∠C的数量关系吗？请说明理由．

查看试题解析
19. 如图，已知A（﹣5，5），B（﹣6，1），C（﹣2，2），将三角形ABC沿AD方向平移，点A平移到点D，点B的对应点为点E，点C的对应点为点F，请完成下列问题：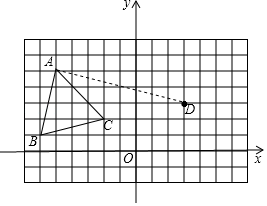

(1)、请在图中作出三角形DEF；点E的坐标为，点F的坐标为；

(2)、若连接AD、BE，则线段AD与线段BE的关系为；

(3)、求三角形ABC的面积．

查看试题解析
20. 某市举行“展运动风采，扬工匠精神”为主题的体育活动，并开展了以下体育项目：足球，乒乓球，篮球和羽毛球，要求参加的市民只能选择一项体育项目．为了了解选择各项体育活动的人数，随机抽取了部分参加体育项目的市民进行调查，并将获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据统计图回答问题：

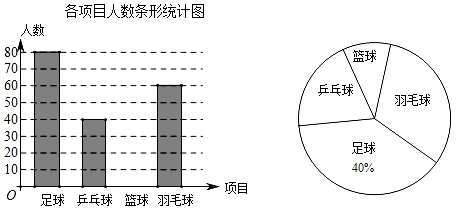(1)、这次活动一共调查了名市民；

(2)、请补全条形统计图；

(3)、羽毛球项目的人数在扇形统计图中所占扇形圆心角的度数是多少度？

(4)、若该市有2500人参加了这次主题活动，请你估计选择乒乓球项目的市民人数约是多少人？

查看试题解析
21. 完成下面推理过程：
如图，已知DE∥BC，DF、BE分别平分∠ADE、∠ABC，可推得∠FDE=∠DEB的理由：

∵DE∥BC（已知）

∴∠ADE=▲ （   ）

∵DF、BE分别平分∠ADE、∠ABC，

∴∠ADF= $\frac{1}{2}$ ▲ （   ）

∠ABE= $\frac{1}{2}$ ▲ （   ）

∴∠ADF=∠ABE

∴▲ ∥▲ （   ）

∴∠FDE=∠DEB.（   ）

查看试题解析
22. 一批货物要运往某地，货主准备租用汽车运输公司的甲、乙两种货车，已知过去两次租用这批货车的情况如表：

第一次
第二次
甲种货车辆数（单位：辆）
2
3
乙种货车辆数（单位：辆）
4
5
累计运货吨数（单位：吨）
18
24.5
现租用该公司4辆甲种货车和5辆乙种货车一次刚好运完这批货，如果按每吨付费30元计算，问货主应付费多少元？

查看试题解析
23. 已知当m，n都是实数，且满足2m＝8+n时，称p（m﹣1， $\frac{n + 2}{2}$ ）为“开心点”．例如点A（5，3）为“开心点”．
因为当A（5，3）时，m﹣1＝5， $\frac{n + 2}{2}$ ＝3，得m＝6，n＝4，
所以2m＝2×6＝12，8+n＝8+4＝12，
所以2m＝8+n．
所以A（5，3）是“开心点”．

(1)、判断点B（4，10）是否为“开心点”，并说明理由；

(2)、若点M（a，2a﹣1）是“开心点”，请判断点M在第几象限？并说明理由．

查看试题解析

	第一次	第二次
甲种货车辆数（单位：辆）	2	3
乙种货车辆数（单位：辆）	4	5
累计运货吨数（单位：吨）	18	24.5