云南省昆明市西山区2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，由AB∥CD，可以得到（）

A、∠1=∠2 B、∠2=∠3 C、∠1=∠4 D、∠D+∠BCD=180°

查看试题解析
2. 西山区今年有14万名七年级学生参加期末考试，为了了解这14万名学生的数学成绩，从中抽取了1000名学生的数学成绩进行统计分析，以下说法正确的是（）

A、这种调查采用了全面调查的方式 B、样本容量为14万 C、1000名学生的数学成绩是总体的一个样本 D、每名学生的数学成绩是样本

查看试题解析
3. 下列等式成立的是（）

A、 $\sqrt{8} = 4$ B、 $\sqrt{(- 3)^{2}} = - 3$ C、 $\sqrt{4} = \pm 2$ D、 $\sqrt[3]{- 27} = - 3$

查看试题解析
4. 已知a＜b，则下列不等关系正确的是（）

A、a+1＜b+1 B、a﹣1＞b﹣1 C、ac＜bc D、 $\frac{a}{c} ＞ \frac{b}{c}$

查看试题解析
5. 为了庆祝中国共产党建党100周年，西山区举行党史知识竞赛，已知竞赛试题共有30道，每一题答对得5分，答错或不答都扣2分，小陈得分要超过100分，则设他答对x道题，则可列不等式正确的是（）

A、5x﹣（30﹣x）＞100 B、5x﹣2（30﹣x）＞100 C、5（30﹣x）﹣2x＞100 D、5（30﹣x）﹣x＞100

查看试题解析
6. 如图，在△ABC中，AC＝8，∠A＝45°，∠B＝105°，把△ABC沿水平向右方向平移到△DEF的位置，若CF＝3，则下列结论中错误的是（）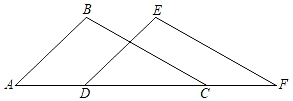

A、AD＝3 B、∠F＝30° C、AB∥DE D、DC＝4

查看试题解析
7. 我国古代很早就对二元一次方程组进行研究，其中不少成果被收入古代数学著作《九章算术》．《九章算术》中的“方程”一章中讲述了算筹图，如图1．图2所示，图中各行从左到右列出的算筹数分别表示未知数xy的系数与相应的常数项．图1表示的算筹图用我们现在所熟悉的方程组形式表述出来为 ${\begin{array}{l} 3 x + 2 y = 11 \\ 4 x + 3 y = 26 \end{array}$ 类似地，图2所示的算筹图我们可以表述为（）

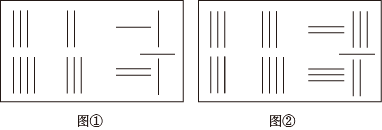A、 ${\begin{array}{l} 2 x + 3 y = 23 \\ 3 x + 4 y = 32 \end{array}$ B、 ${\begin{array}{l} 2 x + 3 y = 23 \\ 3 x + 4 y = 37 \end{array}$ C、 ${\begin{array}{l} 3 x + 2 y = 23 \\ 4 x + 3 y = 37 \end{array}$ D、 ${\begin{array}{l} 11 x + 3 y = 23 \\ 3 x + 4 y = 32 \end{array}$

查看试题解析
8. 如图所示，已知点A（﹣1，2），将长方形ABOC沿x轴正方向连续翻转2021次，点A依次落在点A₁ ， A₂ ， A₃ ， …，A₂₀₂₁的位置，则A₂₀₂₁的坐标是（）

A、（3038，1） B、（3032，1） C、（2021，0） D、（2021，1）

查看试题解析

二、填空题

9. 化简： $\sqrt{\frac{2}{5}}$ =

查看试题解析
10. 在平面直角坐标系中，点A（﹣5，2）在第象限．

查看试题解析
11. 如图，直线a∥b，∠1=120°，则∠2的度数为．

查看试题解析
12. 已知方程 $3 x - y = 5$ ，用含x的代数式表示y，则y= ．

查看试题解析
13. 一个关于x的不等式组的解集在数轴上表示如图，则这个不等式组的解集．

查看试题解析
14. 如图所示，在平面直角坐标系中△ABC中点A的坐标为（﹣1，3），在y轴上有一个点P（0，﹣1），将△ABC在网络线内平移使其顶点与P重合，则平移后A点的对应点的坐标为．

查看试题解析

三、解答题

15. 计算： $\sqrt{9} - \sqrt[3]{27} +$ | $\sqrt{3} -$ 2| $- \sqrt{(- 2)^{2}}$ ．

查看试题解析
16. 已知在平面直角坐标系中，△ABC三个顶点的坐标分别为：A（﹣2，﹣1），B（1，3），C（3，0）．

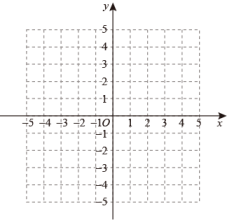(1)、在如下平面直角坐标系中作出△ABC；

(2)、若将△ABC向下平移3个单位后再向左平移2个单位得到△A₁B₁C₁ ，请作出△A₁B₁C₁并写出A₁的坐标．

查看试题解析
17. 解方程组： ${\begin{matrix} 2 x - 3 y = - 5 \\ 3 x + 2 y = 12 \end{matrix}$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 2 (x - 1) ＜ x - 3 \\ \frac{4 x - 5}{3} ＞ x - 1 \end{array}$ ．

查看试题解析
19. 补全下列推理过程
如图，已知EF∥AD，∠1＝∠2，∠BAC＝70°，求∠AGD．
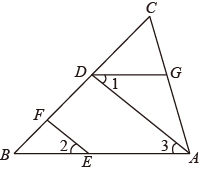
解：∵EF∥AD，
∴∠2＝  ▲  （  ）．
又∵∠1＝∠2（已知），
∴∠1＝∠3（等量代换）．
∴AB∥ ▲  （  ）．
∴∠BAC+  ▲  ＝180°（  ）．
∵∠BAC＝70°，
∴∠AGD＝  ▲   ．

查看试题解析
20. “杂交水稻之父”、“共和国勋章”获得者袁隆平，花费毕生精力，一直在为我们的饥饱操心．他用一己之力，养活了十几亿中国人，我们再也不受食不果腹之苦．某学校为了调查学生对“杂交水稻”知识的了解程度，在全校范围内随机抽取部分学生进行问卷调查，调查结果共分为四个等级：A．非常了解：B．比较了解；C．基本了解；D．不了解．将调查结果整理后绘制成如图所示的不完整的统计图．请你根据图中提供的信息回答下列问题：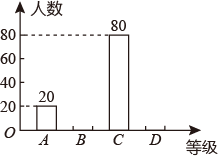

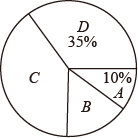(1)、本次调查共抽取了多少名学生？

(2)、直接补全条形统计图；

(3)、若该校共有1200名学生，请你估计该校比较了解“杂交水稻”知识的学生的人数．

查看试题解析
21. 如图，已知AB∥CD，连接BC．点E，F是直线AB上不重合的两点，G是CD上一点，连接ED交BC于点N，连接FG交BC于点M．若∠ENC+∠CMG＝180°．

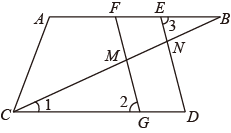(1)、求证：∠2＝∠3；

(2)、若∠A＝∠1+60°，∠ACB＝50°，求∠B的度数．

查看试题解析
22. 习近平总书记说“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气”．某校为提高学生的阅读品味，现决定药买获得十届茅盾文学奖的《北上》《徐则巨著》和《牵风记》两种书．若购买3本《北上》和2本《牵风记》需用165元；购买6本《北上》与购买7本《牵风记》的费用相同．

(1)、求每本《北上》和每本《牵风记》各为多少元；

(2)、该校决定购买以上两种书共50本，总费用不超过1635元，那么该校最多可以购多少本《北上》．

查看试题解析
23. 如图①，在平直角坐标系中，△ABO的三个顶点为A（a，b），B（﹣a，3b），O（0，0），且满足 $\sqrt{a + 3} +$ |b﹣2|＝0，线段AB与y轴交于点C．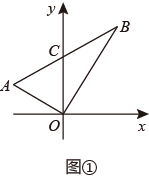

(1)、求出A，B两点的坐标；

(2)、求出△ABO的面积；

(3)、如图②，将线段AB平移至B点的对应点 $B^{'}$ 落在x轴的正半轴上时，此时A点的对应点为 $A^{'}$ ，记△ $A^{'} B^{'} C$ 的面积为S，若24＜S＜32，求点 $A^{'}$ 的横坐标的取值范围．

查看试题解析