云南省昆明市五华区2021年七年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数是无理数的是（）

A、 $\sqrt{4}$ B、3.1415 C、 $3 π$ D、－2

查看试题解析
2. 如图，若在中国象棋盘上建立平面直角坐标系，使“帅”位于点（-1，-1），“马”位于点（2，-1），则“兵”位于点（）

A、 $(- 1 ， 2)$ B、 $(- 3 ， 2)$ C、 $(- 3 ， 1)$ D、 $(- 2 ， 3)$

查看试题解析
3. 郑州市某区为了解参加 $2021$ 年中考的8900名学生的体重情况，随机抽查了其中1500名学生的体重进行统计分析，下列叙述正确的是（）

A、8900名学生是总体 B、每名学生是总体的一个个体 C、1500名学生的体重情况是总体的一个样本 D、以上调查是普查

查看试题解析
4. 如图所示，若 $∠ 1 = 60 °$ ， $∠ 2 = 120 °$ ， $∠ 3 = 70 °$ ，则 $∠ 4$ 的度数是（）

A、70° B、60° C、50° D、40°

查看试题解析
5. 若 $- 2 x^{a} y$ 与 $5 x^{3} y^{b}$ 的和是单项式，则 ${(a + b)}^{2}$ 的平方根是（）

A、2 B、 $\pm 2$ C、4 D、 $\pm 4$

查看试题解析
6. 《算法统宗》中有如下问题：“哑巴来买肉，难言钱数目，一斤少二十五，八两多十五，试问能算者，合与多少肉”，意思是一个哑巴来买肉，说不出钱的数目，买一斤（ $16$ 两）还差二十五文钱，买八两多十五文钱，问肉数和肉价各是多少？设肉价为 $x$ 文/两，哑巴所带的钱数为 $y$ 文，则可建立方程组为（）

A、 ${\begin{array}{l} 16 x = y - 25 \\ 8 x = y + 15 \end{array}$ B、 ${\begin{array}{l} 16 x = y + 25 \\ 8 x = y - 15 \end{array}$ C、 ${\begin{array}{l} 8 x = y - 25 \\ 16 x = y + 15 \end{array}$ D、 ${\begin{array}{l} 8 x = y + 25 \\ 16 x = y - 15 \end{array}$

查看试题解析
7. 为宣传和普及垃圾分类的有效方法，不断增强同学们的环保意识，某学校举办了垃圾分类知识竞赛活动．学校为了解学生对这次大赛的掌握情况，在全校1500名学生中随机抽取部分学生进行了一次问卷调查，并根据收集到的信息进行了统计，绘制了两幅统计图，如图所示．下列四个选项错误的是（）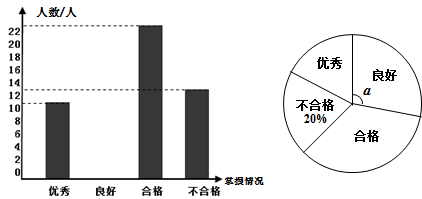

A、样本容量为60 B、所抽取学生中，竞赛成绩“良好”的人数为16人 C、所抽取学生中，成绩为“优秀”和“良好”的人数占比和低于“合格”的人数占比 D、 $α = 96 °$

查看试题解析
8. 若关于 $x$ 的不等式组 ${\begin{array}{l} \frac{x}{2} + \frac{x + 1}{3} > 0 \\ 3 x + 5 a + 4 > 4 (x + 1) + 3 a \end{array}$ 恰有三个整数解，则 $a$ 的取值范围是（）

A、 $1 ⩽ a < \frac{3}{2}$ B、 $1 < a ⩽ \frac{3}{2}$ C、 $1 < a < \frac{3}{2}$ D、 $a ⩽ 1$ 或 $a > \frac{3}{2}$

查看试题解析

二、填空题

9. 端午节期间，食品药品监督管理局对市场上的粽子质量进行了调查，你认为适合采用的调查方式是调查．

查看试题解析
10. 如图，将一块三角板的直角顶点放在直尺的一边上，当 $∠ 2 = 37 °$ 时， $∠ 1 =$ .

查看试题解析
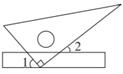11. 已知点P（3a－8，a－1），若点P在y轴上，则点P的坐标为．

查看试题解析
12. 若 ${\begin{array}{l} x = a \\ y = b \end{array}$ 是方程 $2 x - 3 y = 1$ 的一组解，则 $8 - 4 a + 6 b =$ ．

查看试题解析
13. 某次知识竞赛试卷有20道题，评分办法是答对一道记5分，不答记0分，答错一道扣2分，小明有3道题没答，但成绩超过60分，则小明至少答对道题.

查看试题解析
14. 已知，在同一平面内，∠ABC＝50°，AD∥BC，∠BAD的平分线交直线BC于点E，那么∠AEB的度数为．

查看试题解析

三、解答题

15. 解方程组： ${\begin{array}{l} 2 x + y = 13 \\ 4 x - 3 y = 11 \end{array}$

查看试题解析
16. 解不等式组 ${\begin{array}{l} 2 x + 1 \geq 1 \\ \frac{1 + 2 x}{3} ＞ x - 1 \end{array}$ ，并把不等式组的解集在数轴上表示出来.

查看试题解析
17. 在平面直角坐标系中，△ABC经过平移得到三角形△A′B′C′，位置如图所示：

(1)、分别写出点A、A'的坐标：A ， A'；

(2)、若点M（m，n）是△ABC内部一点，则平移后对应点M'的坐标为；

(3)、求△ABC的面积．

查看试题解析
18. 已知5a+2的立方根是3，3a+b-1的算术平方根是4，c是 $\sqrt{13}$ 的整数部分．

(1)、求a，b，c的值；

(2)、求 $3 a - b + c$ 的平方根．

查看试题解析
19. 某中学组织本校数学教师开展线上教学活动，为了解学生线上学习效果，决定随机抽取八年级学生部分学生进行质量测评．试卷满分100分，学生得分设为 $x$ 分．以下是根据测试的数学成绩绘制的统计表和频数分布直方图：

成绩％（分）
频数
频率
第1段
$50 \leq x < 60$
2
0.04
第2段
$60 \leq x < 70$
6
0.12
第3段
$70 \leq x < 80$
9
$b$
第4段
$80 \leq x < 90$
$a$
0.36
第5段
$90 \leq x \leq 100$
15
0.30
请根据所给信息，解答下列问题．

(1)、求 $a$ 和 $b$ ；

(2)、补全频数分布直方图；

(3)、已知该年级有800名学生参加测试，请估计该年级数学成绩为优秀（80分及以上）的人数．

查看试题解析
20. 为了积极推进轨道交通建设，某城市计划修建总长度36千米的有轨电车轨道该任务由甲、乙两工程队先后接力完成，甲工程队每天修建0.06千米，乙工程队每天修建0.08千米，两工程队共需修建500天．求甲、乙两工程队分别修建有轨电车轨道多少千米？

查看试题解析
21. 如图所示，已知直线 $A B$ 与 $C D$ 交于点 $O$ ， $O M ⊥ C D$ 于点 $O$ ， $O A$ 平分 $∠ M O E$ ，且 $∠ B O D = 28 °$ ，求 $∠ C O E$ 的度数．

查看试题解析
22. 每年的6月5日为世界环保日，为了提倡低碳环保，某公司决定购买10台节省能源的新设备，现有甲、乙两种型号的设备可供选购. 经调查：购买3台甲型设备比购买2台乙型设备多花16万元，购买2台甲型设备比购买3台乙型设备少花6万元.

(1)、求甲、乙两种型号设备的价格；

(2)、该公司经预算决定购买节省能源的新设备的资金不超过110万元，你认为该公司有哪几种购买方案；

(3)、在（2）的条件下，已知甲型设备的产量为240吨/月，乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨，为了节约资金，请你为该公司设计一种最省钱的购买方案.

查看试题解析
23. 如图1，已知直线 $A B / /$ 直线 $C D$ ，点 $E$ 在 $A B$ 上，点 $H$ 在 $C D$ 上，点 $F$ 在 $A B$ ， $C D$ 之间，连接 $E F$ ， $F H$ ．

(1)、若 $∠ A E F + ∠ C H F = 280 °$ ，则 $∠ E F H$ 的度数为．

(2)、若 $∠ A E F + ∠ C H F = \frac{11}{4} ∠ E F H$ ．
①求 $∠ E F H$ 的度数；

②如图2，若 $H M$ 平分 $∠ C H F$ ，交 $F E$ 的延长线于点 $M$ ，求 $∠ F H D - 2 ∠ F M H$ 的度数．

查看试题解析

	成绩％（分）	频数	频率
第1段	$50 \leq x < 60$	2	0.04
第2段	$60 \leq x < 70$	6	0.12
第3段	$70 \leq x < 80$	9	$b$
第4段	$80 \leq x < 90$	$a$	0.36
第5段	$90 \leq x \leq 100$	15	0.30