安徽省芜湖市2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列属于无理数的是（）．

A、 $\sqrt{4}$ B、 $\sqrt[3]{64}$ C、 $(\sqrt{3})^{2}$ D、 $π - 1$

查看试题解析
2. 在平面直角坐标系中，有 $C (1 ， 2) ，$ $D (1 ， - 1)$ 两点，则点C可由点D（）

A、向上平移3个单位长度得到 B、向下平移3个单位长度得到 C、向左平移1个单位长度得到 D、向右平移1个单位长度得到

查看试题解析
3. 下列图形中，由∠1＝∠2能推得AB∥CD的是（）．

A、 B、 C、 D、

查看试题解析
4. 将不等式组 ${\begin{array}{l} x \geq - 2 \\ x < 1 \end{array}$ 的解集在数轴上表示如下，正确的是（）．

A、 B、 C、 D、

查看试题解析
5. 某校为了了解初一年级1200名学生的视力情况，从中随机抽取了300名学生进行视力情况的调查，下列说法错误的是（）

A、总体是1200名学生的视力情况 B、样本容量是300 C、样本是抽取的300名学生 D、个体是每名学生的视力情况

查看试题解析
6. 若方程mx-2y=3x+4是关于x，y的二元一次方程，则m的取值范围是（）

A、m≠0 B、m≠3 C、m≠-3 D、m≠2

查看试题解析
7. 在平面直角坐标系中有点A（－1，3）和点B，且AB＝2，则点B不可能在（）．

A、第一象限 B、x轴上 C、第二象限 D、y轴上

查看试题解析
8. 已知 $a < b$ ，下列式子不一定成立的是（）

A、 $a - 1 < b - 1$ B、 $- 2 a > - 2 b$ C、 $\frac{1}{2} a + 1 < \frac{1}{2} b + 1$ D、 $m a > m b$

查看试题解析
9. 如图， $A B / / D E$ ，那么 $∠ B C D =$ （）

A、 $180 ° + ∠ 1 - ∠ 2$ B、 $∠ 1 + ∠ 2$ C、 $∠ 2 - ∠ 1$ D、 $180 ° + ∠ 2 - 2 ∠ 1$

查看试题解析
10. 关于x的不等式 ${\begin{array}{l} x - m > 0 \\ 7 - 2 x > 1 \end{array}$ 的整数解只有4个，则m的取值范围是（）

A、 $- 2 < m \leq - 1$ B、 $- 2 \leq m \leq - 1$ C、 $- 2 \leq m < - 1$ D、 $- 3 < m \leq - 2$

查看试题解析

二、填空题

11. $\sqrt{2} - 1$ 的相反数是．

查看试题解析
12. 已知三个数a﹣1，3﹣a，2a在数轴上所对应的点从左到右依次排列，那么a的取值范围是．

查看试题解析
13. 如图，将一张长方形纸片沿 $E F$ 折叠后，点 $C$ ， $D$ 分别落在 $C^{'}$ ， $D^{'}$ 的位置，若 $∠ E F B = 65 °$ ，则 $∠ A E D^{^{'}}$ 的度数为．

查看试题解析
14. 在如图所示的长方形中放置了8个形状、大小都相同的小长方形，则图中阴影部分的面积为．

查看试题解析
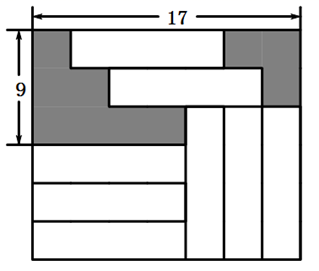15. 已知点A（－2，0），B（0，4）和C（m＋1，2－m）．

(1)、当BC∥x轴时，则B，C两点之间的距离为；

(2)、若P是y轴上一点，且满足S_△APB＝ $\frac{1}{2}$ S_△AOB ，则点P的坐标为．

查看试题解析

三、解答题

16. 解方程组 ${\begin{array}{l} x - y = 4 \\ 4 x + 2 y = - 1 \end{array}$ .

查看试题解析
17. 解不等式： $\frac{2 x - 1}{3} - \frac{5 x + 1}{2}$ ≤1.

查看试题解析
18. 全球气候变暖导致一些冰川融化并消失．在冰川消失12年后，一种低等植物苔藓就开始在岩石上生长．每一个苔藓都会长成近似圆形，苔藓的直径和冰川消失后经过的时间近似地满足如下的关系式：d＝7× $\sqrt{t - 12}$ （t≥12）．其中d代表苔藓的直径，单位是厘米；t代表冰川消失后经过的时间，单位是年．

(1)、计算冰川消失16年后苔藓的直径；

(2)、如果测得一些苔藓的直径是35厘米，问冰川约是在多少年前消失的？

查看试题解析
19. 如图所示的方格纸中每个小方格都是边长为1个单位的正方形，建立如图所示的平面直角坐标系，已知点A（1，0），B（4，0），C（3，3），D（1，4）．

(1)、顺次连接点A、B、C、D、A，画出四边形ABCD；

(2)、画出把四边形ABCD向左平移5个单位，再向下平移2个单位得到的四边形A′B′C′D′；

(3)、直接写出四边形A′B′C′D′的面积是．

查看试题解析
20. 如图，是一个运算流程：

(1)、分别计算：当x＝2时，y＝；当x＝－2时，y＝；

(2)、若需要经过两次运算，才能运算出y，求x的取值范围．

查看试题解析
21. 某中学初二年级抽取部分学生进行跳绳测试．并规定：每分钟跳90次以下的为不及格；每分钟跳90～99次的为及格；每分钟跳100～109次的为中等；每分钟跳110～119次的为良好；每分钟跳120次及以上的为优秀．测试结果整理绘制成如下两幅不完整的统计图．请根据图中信息，解答下列各题：

(1)、参加这次跳绳测试的共有人；

(2)、补全条形统计图；

(3)、在扇形统计图中，“中等”部分所对应的圆心角的度数是；

(4)、如果该校初二年级的总人数是480人，根据此统计数据，请你估算该校初二年级跳绳成绩为“优秀”的人数．

查看试题解析
22. 如图，AE⊥BC于点M，DF⊥BC于点N，且∠1＝∠2．

(1)、判断AB与CD是否平行，并请说明理由；

(2)、若BC平分∠ABD，且∠BDC＝∠3＋90°，求∠C的度数．

查看试题解析
23. 为了更好治理西太湖水质，保护环境，市治污公司决定购买10 台污水处理设备，现有A、B两种型号的设备，其中每台的价格，月处理污水量如下表：
经调查：购买-台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买4台B型设备少4万元.

(1)、求a、b的值；

(2)、经预算：市治污公司购买污水处理设备的资金不超过47万元，并且该月要求处理西太湖的污水量不低于1860 吨，则有哪几种购买方案?请指出最省钱的一种购买方案，并指出相应的费用.

查看试题解析