安徽省马鞍山市2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-06-29 类型:期末考试
一、单选题
-
1. 下列实数中,最小的数是( )A、 B、 C、0 D、12. 下列计算正确的是( )A、 B、 C、 D、3. 使分式 在实数范围内有意义,则实数m的取值范围是( )A、m≠1 B、m≠3 C、m=3 D、m=14. 下列说法错误的是( )A、由 , 可得 B、由 , 可得 C、由 , 可得 D、由 , 可得5. 下列说法中正确的是( )A、无限不循环小数都是无理数 B、绝对值最小的实数不存在 C、是最小的正无理数 D、有理数与数轴上的点一一对应6. 如图,若∥ , 则下列结论中正确的是( )
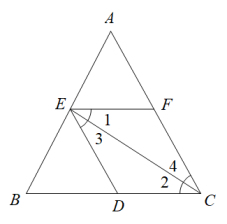 A、 B、 C、 D、7. 如果是一个完全平方式,那么的值是( )A、3 B、 C、9 D、8. 如图,将木条 , 与钉在一起, , , 要使木条与平行,木条顺时针旋转的度数至少是( )
A、 B、 C、 D、7. 如果是一个完全平方式,那么的值是( )A、3 B、 C、9 D、8. 如图,将木条 , 与钉在一起, , , 要使木条与平行,木条顺时针旋转的度数至少是( )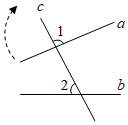 A、 B、 C、 D、9. 如图,两个正方形的边长分别为a和b,如果a+b=10,ab=22,那么阴影部分的面积是( )
A、 B、 C、 D、9. 如图,两个正方形的边长分别为a和b,如果a+b=10,ab=22,那么阴影部分的面积是( ) A、15 B、17 C、20 D、2210. 若关于的方程的解是正数,则的取值范围为( )A、 B、 C、且 D、且
A、15 B、17 C、20 D、2210. 若关于的方程的解是正数,则的取值范围为( )A、 B、 C、且 D、且二、填空题
-
11. 方程的解是 .12. 已知 , 则的值是;13. 分解因式: .14. 如图,AB⊥l1 , AC⊥l2 , 垂足分别为B,A,则A点到直线l1的距离是线段的长度.
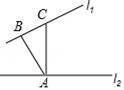 15. 无论取何值,总成立,则的值为 .16. 已知 , 则的值是 .17. 一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=.
15. 无论取何值,总成立,则的值为 .16. 已知 , 则的值是 .17. 一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=. 18. 对一个实数x 按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“结果是否大于88?"为一次操作.如果操作进行了两次就停止,则x的取值范围是
18. 对一个实数x 按如图所示的程序进行操作,规定:程序运行从“输入一个实数x”到“结果是否大于88?"为一次操作.如果操作进行了两次就停止,则x的取值范围是
三、解答题
-
19. 解不等式组 ,并写出它的正整数解.20. 先化简,再求值: , 其中 .21. 如图:
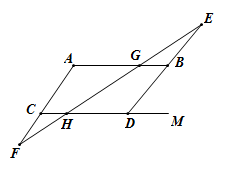 (1)、写出图中的同位角:;(2)、如果∥ , 那么图中与相等的角有个(除外);(3)、当时,∥ , 理由:;(4)、如果与互补,那么与有什么关系?说明理由.22. 观察以下等式:
(1)、写出图中的同位角:;(2)、如果∥ , 那么图中与相等的角有个(除外);(3)、当时,∥ , 理由:;(4)、如果与互补,那么与有什么关系?说明理由.22. 观察以下等式:;
;
;
…
(1)、按以上等式的规律,填空:( ▲ );(2)、利用(1)中的公式,计算: .23. 某高速铁路一路段正在建设中,甲、乙两个工程队计划参与其中一项工程建设,甲队单独施工30天,恰好完成了该项工程的 , 若这时乙队加入,则两队还需同时施工15天,才能完成该项工程.(请用方程或不等式的知识解决以下问题)(1)、若乙队单独施工,需要多少天才能完成该项工程?(2)、若甲队参与该项工程施工的时间不超过36天,则乙队至少还需施工多少天才能完成该项工程?(请用方程或不等式知识解答以下问题)24.(1)、将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.例如: .①分解因式:;
②若都是正整数且满足 , 求的值;
(2)、若为实数且满足 , , 求的最小值.