安徽省六安市霍邱县2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式在实数范围内没有意义的是（）

A、 $- \sqrt{3}$ B、 $\sqrt{- 3}$ C、 $\sqrt{(- 3)^{2}}$ D、 $\sqrt{0}$

查看试题解析
2. 若m＞n，则下列不等式成立的是（）

A、m﹣7＜n﹣7 B、3m＜3n C、﹣5m＞﹣5n D、 $\frac{m}{9} > \frac{n}{9}$

查看试题解析
3. 下面的计算正确的是（）

A、x³•x³＝2x³ B、（x³）²＝x⁵ C、（6xy）²＝12x²y² D、（﹣x）⁴÷（﹣x）²＝x²

查看试题解析
4. 据报道，中国医学研究人员通过研究获得了纯化灭活新冠病毒疫苗，该疫苗在低温电镜下呈椭圆形颗粒，最小直径约为90nm，已知1nm＝10^﹣⁹m，则90nm用科学记数法表示为（）

A、0.09×10^﹣⁶m B、0.9×10^﹣⁷m C、9×10^﹣⁸m D、90×10^﹣⁹m

查看试题解析
5. 不等式 $\frac{4 + x}{3} - 1 \leq \frac{x}{2}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 若k为正整数，则 ${(\underset{k 个 k}{\underset{︸}{k + k + \cdot \cdot \cdot + k}})}^{k} =$ （）

A、 $k^{2 k}$ B、 $k^{2 k + 1}$ C、 $2 k^{k}$ D、 $k^{2 + k}$

查看试题解析
7. 如图，工人师傅用角尺画出工件边缘AB的垂线a和b，得到a∥b，理由是（）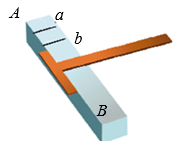

A、连结直线外一点与直线上各点的所有线段中，垂线段最短 B、在同一平面内，垂直于同一条直线的两条直线互相平行 C、在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线 D、经过直线外一点，有且只有一条直线与这条直线平行

查看试题解析
8. 若 $\frac{6}{2 x + 3}$ 表示一个整数，则整数x可取值的个数是（）

A、2个 B、3个 C、4个 D、8个

查看试题解析
9. 如图，已知CD⊥AB，EF⊥AB，垂足分别为D、F，下列条件不能推出∠ADG＝∠B的是（）

A、∠2＝∠3 B、∠1＝∠3 C、∠1＝∠2 D、∠DGC+∠ACB＝180°

查看试题解析
10. 已知关于x的分式方程 $\frac{10 x - 3}{3 - x} = \frac{k - 27}{x - 3} - 3$ 的解满足2＜x＜5，则k的取值范围是（）

A、﹣7＜k＜14 B、﹣7＜k＜14且k≠0 C、﹣14＜k＜7且k≠0 D、﹣14＜k＜7

查看试题解析

二、填空题

11. 若 $\sqrt{21}$ 在两个相邻整数a，b之间，则a+b＝．

查看试题解析
12. 如图，已知直线a，b被直线c所截，且a//b，若∠α＝40°，则∠β的度数为．

查看试题解析
13. 按照如图所示的流程图，若输出的M＝6，则输入的m是．

查看试题解析
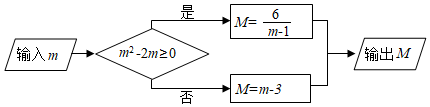14. 如图，一个长方形的长为a，宽为b，将它剪去一个正方形①，然后从剩余的长方形中再剪去一个正方形③，最后剩下长方形②．请用含a、b的代数式表示：

(1)、正方形③的边长为．

(2)、长方形②的面积为．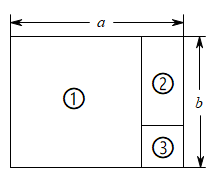

查看试题解析

三、解答题

15.

(1)、计算： $\sqrt{4} - {(\frac{1}{2})}^{- 1} + (π - 3)^{0}$ ；

(2)、因式分解：2x³﹣32x．

查看试题解析
16. 如图，在5×5的正方形网格中，每个小正方形的边长均为1，三角形ABC的A、B、C三个顶点都在格点（网格线的交点）上．

(1)、已知点F在格点上，将三角形ABC平移，得到三角形DEF，使A与D，B与E，C与F分别对应，画出三角形DEF；

(2)、连接AD，连接CF、BE，若AD＝m，则四边形CFEB的周长是多少？（用含m的式子表示）

查看试题解析
17. 先化简，再求值： $(\frac{a^{2} - 4}{a^{2} - 4 a + 4} - \frac{1}{a - 2}) \div \frac{a + 1}{a + 2}$ ，其中a＝﹣1．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 5 x - 2 > 7 x - 4 \\ \frac{2 x - 1}{3} \leq \frac{3 x + 1}{2} \end{array}$ ，并写出满足条件的所有整数解．

查看试题解析
19. 观察下面的图形及对应的等式：①1²＝0²+1；②2²＝1²+3；③3²＝2²+5；④4²＝3²+7；

(1)、根据上面的规律，写出第⑦个等式：．

(2)、猜想第n个等式（用含n的代数式表示），并验证你的猜想是正确的．

查看试题解析
20. 如图是某公司的一份进货单，该公司会计欲查询乙商品的进价，发现进货单已被墨水污染．于是，会计向商品采购员和仓库保管员了解情况．
进货单
进价
数量（元/件）
总金额（件）
商品名称（元）
甲
7200.00
乙
3200.00
商品采购员李阿姨和仓库保管员王师傅对采购情况回忆如下：李阿姨：我记得甲商品进价比乙商品进价每件高50%；王师傅：甲商品比乙商品的数量多40件．请你根据上面的信息，求出乙商品的进价，并帮助他们补全进货单．

查看试题解析
21. 在小学，我们已经知道三角形的三个内角的和等于180°，现在我们可以用所学的平行线的相关知识来说明它．如图，已知三角形ABC．

(1)、读语句，画图形：在图中，过点A作直线MN，使MN//BC；

(2)、请利用（1）中的图形说明∠A+∠B+∠C＝180°．

查看试题解析
22. 为了支持贫困地区发展，某企业需运输一批扶贫物资．据调查得知，2辆大货车与4辆小货车一次可以运输1000箱物资；5辆大货车与2辆小货车一次可以运输1300箱物资．

(1)、求1辆大货车和1辆小货车一次分别可以运输多少箱物资？

(2)、该企业计划用两种货车共12辆运输这批物资，每辆大货车一次需费用500元，每辆小货车一次需费用300元，若一次运输物资不少于2200箱，且总费用小于5600元，请你列出所有运输方案，并指出哪种运输方案所需总费用最少，最少总费用是多少？

查看试题解析
23. 已知：如图，AB//CD//GH，GH过点P．

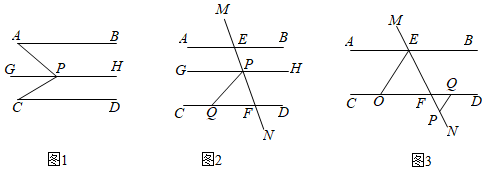(1)、如图1，若∠BAP＝40°，∠DCP＝30，则∠APC＝（直接写出结果）；

(2)、如图2，直线MN分别交AB于点E，交CD于点F，点P在线段EF上，点Q在射线FC上．若∠MEB＝110°，∠PQF＝50°，求∠EPQ的度数；

(3)、如图3，点P在射线FN上，点Q在射线FD上， $∠$ AEF的平分线交CD于点O．若 $∠ P Q F = \frac{1}{2} ∠ M E B$ ，试判断OE与PQ是否平行？并说明理由．

查看试题解析

进价	数量（元/件）	总金额（件）	商品名称（元）
甲			7200.00
乙			3200.00