安徽省淮北市2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列说法错误的是（）

A、 $\frac{1}{25}$ 的平方根是± $\frac{1}{5}$ B、﹣9是81的平方根 C、0.4的算术平方根是0.2 D、 $\sqrt[3]{- 27}$ ＝﹣3

查看试题解析
2. 下列不等式变形正确的是 $()$

A、由 $a > b$ ，得 $a c > b c$ B、由 $a > b$ ，得 $- 2 + a < b - 2$ C、由 $- \frac{1}{2} > - 1$ ，得 $- \frac{a}{2} > - a$ D、由 $a > b$ ，得 $c - a < c - b$

查看试题解析
3. 某种计算机完成一次基本运算的时间约为1纳秒 $(n s)$ ，已知1纳秒 $= 0.000 000 001$ 秒，该计算机完成15次基本运算，所用时间用科学记数法表示为（）

A、 $1.5 \times 10^{- 9}$ 秒 B、 $15 \times 10^{- 3}$ 秒 C、 $1.5 \times 10^{- 8}$ 秒 D、 $15 \times 10^{- 8}$ 秒

查看试题解析
4. 下列因式分解正确的是（）

A、（a-3）²=a²-6a+9 B、-4a+a²=-a（4+a） C、a²+4a+4=（a+2）² D、a²-2a+1=a（a-2）+1

查看试题解析
5. 如果分式 $\frac{| x | - 1}{x + 1}$ 的值为0，那么 $x$ 的值为（）

A、-1 B、1 C、-1或1 D、1或0

查看试题解析
6. 点P为直线 $l$ 外一点：点A、B、C为直线 $l$ 上三点，PA＝4 cm，PB＝5 cm，PC＝2 cm，则点P到直线 $l$ 的距离是（）

A、2 cm B、4 cm C、5 cm D、不超过2 cm

查看试题解析
7. 将分式 $\frac{x^{2} y}{x - y}$ 中的x，y的值同时扩大为原来的3倍，则分式的值（）

A、扩大6倍 B、扩大9倍 C、不变 D、扩大3倍

查看试题解析
8. 如图，两个一样的直角三角形重叠在一起，将其中一个三角形沿着点 $B$ 到点 $C$ 的方向平移到三角形 $D E F$ 的位置， $∠ B = 90 °$ ， $A B = 10$ ， $D H = 4$ ，平移距离为7，求阴影部分的面积为（）

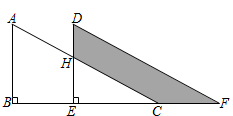A、56 B、54 C、52 D、50

查看试题解析
9. 我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”（如图），此图揭示了（a+b）n（n为非负整数）展开式的项数及各项系数的有关规律．
例如：
（a+b）⁰＝1
（a+b）¹＝a+b
（a+b）²＝a²+2ab+b²
（a+b）³＝a³+3a²b+3ab²+b³
（a+b）⁴＝a⁴+4a³b+6a²b²+4ab³+b⁴
…
请你猜想（a+b）⁹的展开式中所有系数的和是（）

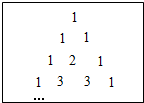A、2018 B、512 C、128 D、64

查看试题解析
10. 给出下列说法：
⑴两条直线被第三条直线所截，同位角相等；
⑵过平面内一点有且只有一条直线与已知直线平行；
⑶相等的两个角是对顶角；
⑷从直线外一点到这条直线的垂线段，叫做这点到直线的距离；
⑸不相交的两条直线叫做平行线；
⑹垂直于同一条直线的两条直线平行．
其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

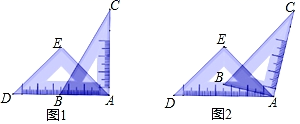
11. 若关于 $x$ 的分式方程 $\frac{3 x}{x - 2} - 1 = \frac{m + 3}{x - 2}$ 有增根，则 $m$ 的值为.

查看试题解析
12. 若9x²+kx+1是一个完全平方式，则k= ．

查看试题解析
13. 若 $\frac{1}{x} + \frac{1}{y} = 2$ ，则 $\frac{2 x + x y + 2 y}{3 x + 5 x y + 3 y} =$ ．

查看试题解析
14. 一副直角三角尺叠放如图1所示，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动（旋转角不超过180度），使两块三角尺至少有一组边互相平行.如图2：当∠BAD＝15°时，BC∥DE.则∠BAD（0°＜∠BAD＜180°）其它所有可能符合条件的度数为.

查看试题解析

三、解答题

15. $\sqrt[3]{{(- 5)}^{3}} + {(- 3)}^{2} - \sqrt{25} + | \sqrt{3} - 2 | + {(\sqrt{3})}^{2}$

查看试题解析
16. 先化简： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，再从 $- 1 \leq x \leq 2$ 的范围内选取一个合适的整数作为 $x$ 的值代入求值.

查看试题解析
17. 从边长为 $a$ 的正方形中剪掉一个边长为 $b$ 的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）.

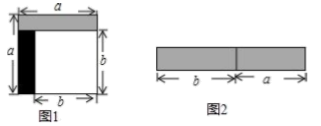(1)、上述操作能验证的等式是；（请选择正确的一个）
A、 $a^{2} - 2 a b + b^{2} = (a - b)^{2}$ ，
B、 $a^{2} - b^{2} = (a + b) (a - b)$ ，
C、 $a^{2} + a b = a (a + b)$ .

(2)、应用你从（1）选出的等式，完成下列各题：①已知 $x^{2} - 4 y^{2} = 12$ ， $x + 2 y = 4$ ，求 $x - 2 y$ 的值.
②计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) ⋯ (1 - \frac{1}{4 9^{2}}) (1 - \frac{1}{5 0^{2}})$ .

查看试题解析
18. 已知 $2^{m} = 3$ ， $2^{n} = 5$ ，求 $2^{4 m - 2 n}$ 的值．

查看试题解析
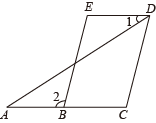
19. 阅读下面的文字，解答问题：大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部地写出来，于是小明用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，事实上，小明的表示方法是有道理的，因为 $\sqrt{1} < \sqrt{2} < \sqrt{4}$ ，所以 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分，请据此解答：

(1)、 $\sqrt{11}$ 的整数部分是，小数部分是；

(2)、如果 $\sqrt{7}$ 的小数部分为 $a$ ， $\sqrt{41}$ 的整数部分为 $b$ ，求 $a + b - \sqrt{7}$ 的值；

(3)、若设 $2 + \sqrt{3}$ 的整数部分为 $x$ ，小数部分为 $y$ ，求 $y - x$ 的值．

查看试题解析
20. 完成下面的证明．（在括号中注明理由）
已知：如图，BE∥CD，∠A＝∠1，
求证：∠C＝∠E．
证明：∵BE∥CD，（已知）
∴∠2＝∠C，（  ）
又∵∠A＝∠1，（已知）
∴AC∥  ▲   ，（  ）
∴∠2＝  ▲   ，（  ）
∴∠C＝∠E（等量代换）

查看试题解析
21. 某市为创建全国文明城市，开展“美化绿化城市”活动，计划经过若干年使城区绿化总面积新增360万平方米.自2015年初开始实施后，实际每年绿化面积是原计划的1.6倍，这样可提前4年完成任务.

(1)、实际每年绿化面积为多少万平方米？

(2)、为加大创建力度，市政府决定从2018年起加快绿化速度，要求不超过2年完成，那么实际平均每年绿化面积至少还要增加多少万平方米？

查看试题解析
22. 如图，已知AM//BN， $∠ A = 60 °$ ，点 $P$ 是射线 $A M$ 上一动点（与点 $A$ 不重合）， $B C$ 、 $B D$ 分别平分 $∠ A B P$ 和 $∠ P B N$ ，分别交射线 $A M$ 于 $C$ 、 $D$ ．

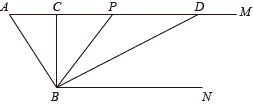(1)、求 $∠ C B D$ 的度数；

(2)、在点P的运动过程中，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．

(3)、当点P运动到使∠ACB=∠ABD时，求∠ABC的度数是 ▲ ，并说明理由．

查看试题解析