安徽省合肥市巢湖市2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-06-29 类型:期末考试
一、单选题
-
1. 在下列各数中,是无理数的是( )A、﹣2 B、π C、3.1415 D、2. 如果a>b,那么下列不等式成立的是( )A、a﹣b<0 B、a﹣3<b﹣3 C、 D、﹣3a<﹣3b3. 下列调查方式合适的是( )A、为了了解电视机的使用寿命,采用全面调查的方式 B、为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 C、调查某中学七年级一班学生视力情况,采用抽样调查的方式 D、为了了解巢湖水资源质量,采用抽样调查的方式4. 如图所示,∠1和∠2是对顶角的是( )A、
 B、
B、 C、
C、 D、
D、 5. 不等式组 的解集在数轴上表示为( )A、
5. 不等式组 的解集在数轴上表示为( )A、 B、
B、 C、
C、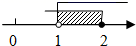 D、
D、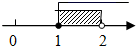 6. 如图,直线a∥b,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为( )
6. 如图,直线a∥b,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为( )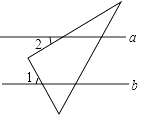 A、30° B、32° C、42° D、58°7. 如图所提供的信息正确的是( ).
A、30° B、32° C、42° D、58°7. 如图所提供的信息正确的是( ). A、七年级学生最多 B、八年级比九年级的学生多 C、九年级学生女生比男生多 D、九年级的男生是女生的两倍8. 《九章算术》是中国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系,在其方程章中有一道题:今有甲乙二人,不知其钱包里有多少钱,若乙把其钱的一半给甲,则甲的钱数为50;若甲把其钱的 给乙,则乙的钱数也能为50,问甲、乙各有多少钱?若设甲持钱为x,乙持钱为y,则可列方程组
A、七年级学生最多 B、八年级比九年级的学生多 C、九年级学生女生比男生多 D、九年级的男生是女生的两倍8. 《九章算术》是中国古代第一部数学专著,它的出现标志着中国古代数学形成了完整的体系,在其方程章中有一道题:今有甲乙二人,不知其钱包里有多少钱,若乙把其钱的一半给甲,则甲的钱数为50;若甲把其钱的 给乙,则乙的钱数也能为50,问甲、乙各有多少钱?若设甲持钱为x,乙持钱为y,则可列方程组 A、 B、 C、 D、9. 某种商品的进价为80元,出售时的标价为120元,后来由于该商品积压,商店准备打折出售,但要保证利润率不低于5%,则至多打( )A、九折 B、八折 C、七折 D、六折10. 如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G,则图中与∠ECB相等的角有( )
A、 B、 C、 D、9. 某种商品的进价为80元,出售时的标价为120元,后来由于该商品积压,商店准备打折出售,但要保证利润率不低于5%,则至多打( )A、九折 B、八折 C、七折 D、六折10. 如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G,则图中与∠ECB相等的角有( ) A、6个 B、5个 C、4个 D、3个
A、6个 B、5个 C、4个 D、3个二、填空题
-
11. 比较大小:3 (填写“<”或“>”)12. 已知是方程3mx﹣y=﹣1的解,则m= .13. 已知A(a,0),B(﹣3,0)且AB=7,则a=.14. 如图,在平面直角坐标系中:A(1,1),B(﹣1,1),C(﹣1,﹣3),D(1,﹣3),现把一条长为2021个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→……的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是 .

三、解答题
-
15. 计算: .16. 解不等式 , 并写出它的正整数解.17. 已知:如图, , 求证: .
 18. 阅读下列材料,解答问题:
18. 阅读下列材料,解答问题:我们知道是无理数,而无理数是无限不循环小数,它的小数部分我们不可能全部地写出来,但是由于1<<2,所以的整数部分为1,小数部分为﹣1.根据以上的内容,解答下面的问题:如果的小数部分为a,的整数部分为b,求:a+b﹣的值.
19. 如图,在平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1 , 点P的对应点为P1(a+5,b﹣3). (1)、直接写出点C1的坐标;(2)、在图中画出△A1B1C1;(3)、求△AOA1的面积.20. 某学校为了加强训练学生的篮球和足球运球技能,准备购买一批篮球和足球用于训练,已知购买1个篮球和2个足球共需316元;购买2个篮球和3个足球共需534元.(1)、购买1个篮球和1个足球各需多少元?(2)、学校准备购进篮球和足球共40个,并且总费用不超过4200元,则篮球最多可购买多少个?21. 近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其它,该小组对某超市一天内购物者的支付方式进行调查统计,得到如下两幅不完整的统计图.
(1)、直接写出点C1的坐标;(2)、在图中画出△A1B1C1;(3)、求△AOA1的面积.20. 某学校为了加强训练学生的篮球和足球运球技能,准备购买一批篮球和足球用于训练,已知购买1个篮球和2个足球共需316元;购买2个篮球和3个足球共需534元.(1)、购买1个篮球和1个足球各需多少元?(2)、学校准备购进篮球和足球共40个,并且总费用不超过4200元,则篮球最多可购买多少个?21. 近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其它,该小组对某超市一天内购物者的支付方式进行调查统计,得到如下两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)、本次一共调查了多少名购物者?(2)、请补全条形统计图;在扇形统计图中C种支付方式所对应的圆心角为 ▲ 度.(3)、若该超市这一周内有2200名购物者,请估计使用A和B两种支付方式的购物者约有多少名?22. 如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移4个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB. (1)、求点C,D的坐标及四边形ABDC的面积S四边形ABCD;(2)、在y轴上是否存在一点M,连接MC,MD,使S△MCD=S平行四边形ABCD?若存在这样的点,求出点M的坐标,若不存在,试说明理由.23. 问题情景:如图1,AB∥CD,∠PAB=140°,∠PCD=135°,求∠APC的度数.
(1)、求点C,D的坐标及四边形ABDC的面积S四边形ABCD;(2)、在y轴上是否存在一点M,连接MC,MD,使S△MCD=S平行四边形ABCD?若存在这样的点,求出点M的坐标,若不存在,试说明理由.23. 问题情景:如图1,AB∥CD,∠PAB=140°,∠PCD=135°,求∠APC的度数. (1)、丽丽同学看过图形后立即口答出:∠APC=85°,请补全她的推理依据.
(1)、丽丽同学看过图形后立即口答出:∠APC=85°,请补全她的推理依据.如图2,过点P作PE∥AB,
因为AB∥CD,所以PE∥CD.( )
所以∠A+∠APE=180°,∠C+∠CPE=180°.( )
因为∠PAB=140°,∠PCD=135°,所以∠APE=40°,∠CPE=45°,
∠APC=∠APE+∠CPE=85°.
(2)、问题迁移:如图3,AD∥BC,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β,求∠CPD与∠α、∠β之间有什么数量关系?请说明理由.
(3)、在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请直接写出∠CPD与∠α、∠β之间的数量关系.