安徽省滁州市2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-06-29 类型:期末考试
一、单选题
-
1. 下列图案可以通过一个“基本图形”平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在0, ,π,﹣ , ﹣5中,无理数的个数是( )A、1 B、2 C、3 D、43. 下列计算正确的是( )A、 B、 C、 D、4. 据生物学可知,有一种细胞的直径为0.000025米,数据0.000025用科学记数法表示为( )A、2.5×10﹣5 B、2.5×10﹣4 C、0.25×10﹣4 D、0.25×10﹣35. 若一个正数的两个平方根分别是2m+6和m﹣18,则5m+7的立方根是( )A、9 B、3 C、±2 D、﹣96. 不等式组 的解集在数轴上表示正确的是( )A、
2. 在0, ,π,﹣ , ﹣5中,无理数的个数是( )A、1 B、2 C、3 D、43. 下列计算正确的是( )A、 B、 C、 D、4. 据生物学可知,有一种细胞的直径为0.000025米,数据0.000025用科学记数法表示为( )A、2.5×10﹣5 B、2.5×10﹣4 C、0.25×10﹣4 D、0.25×10﹣35. 若一个正数的两个平方根分别是2m+6和m﹣18,则5m+7的立方根是( )A、9 B、3 C、±2 D、﹣96. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、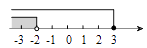 C、
C、 D、
D、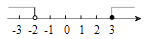 7. 下列因式分解正确的是( )A、3ab2﹣6ab=3a(b2﹣2b) B、x(a﹣b)﹣y(b﹣a)=(a﹣b)(x﹣y) C、a2+2ab﹣4b2=(a﹣2b)2 D、﹣a2+a﹣=﹣(2a﹣1)28. 如图,直线ME交直线AB于点M,交直线CD于点E,MN平分∠BME,∠1=∠2=40°,则∠3的度数是( )
7. 下列因式分解正确的是( )A、3ab2﹣6ab=3a(b2﹣2b) B、x(a﹣b)﹣y(b﹣a)=(a﹣b)(x﹣y) C、a2+2ab﹣4b2=(a﹣2b)2 D、﹣a2+a﹣=﹣(2a﹣1)28. 如图,直线ME交直线AB于点M,交直线CD于点E,MN平分∠BME,∠1=∠2=40°,则∠3的度数是( ) A、120° B、110° C、100° D、95°9. 某品牌自行车的标价比成本价高20% ,根据市场需求,该自行车需降价x% ,若保证不亏本,则x应满足( )A、x≤ B、x≤25 C、x< D、x<10. 关于x的分式方程=﹣1的解是正数,则m的取值范围是( )A、m>﹣2 B、m<﹣2 C、m>﹣2且m≠2 D、m<﹣2且m≠﹣2
A、120° B、110° C、100° D、95°9. 某品牌自行车的标价比成本价高20% ,根据市场需求,该自行车需降价x% ,若保证不亏本,则x应满足( )A、x≤ B、x≤25 C、x< D、x<10. 关于x的分式方程=﹣1的解是正数,则m的取值范围是( )A、m>﹣2 B、m<﹣2 C、m>﹣2且m≠2 D、m<﹣2且m≠﹣2二、填空题
-
11. 的算术平方根是.12. 已知ab=5,a﹣b=﹣2,则﹣a2b+ab2= .13. 已知关于x的不等式组 的整数解只有3个,则m的取值范围是14. 一副直角三角尺按如图①所示的方式叠放,现将含45°角三角尺ADE固定不动,将含30°角的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行;如图②,当∠BAD=15°时,BC//DE,则∠BAD(0°<∠BAD<90°)其他所有可能符合条件的度数为 .

三、解答题
-
15. 计算:(1)、﹣﹣(﹣)﹣2+(π﹣3)0 .(2)、[a3•a5+(3a4)2]÷a2 .16. 规定的运算法则是=ad﹣bc,如=2×5﹣3×1=7.(1)、计算;(2)、若<﹣2,求x的取值范围.17. 解方程:﹣= .18. 如图, , , 垂足分别是 , , 直线分别交 , 于点 , .
 (1)、和相等的角有;(2)、若 , 求的度数.19. 先化简,再求值:()÷ , 其中a为整数,且a满足2≤a<5.20. 已知关于x,y的方程组的解满足x≥0,y<0.(1)、求m的取值范围;(2)、在m的取值范围内,当m取何整数时,不等式(2m+1)x<2m+1的解集为x>1?21. 观察下列等式:①1﹣1﹣=﹣;②﹣﹣=﹣;③﹣﹣=﹣;④﹣﹣=﹣;⑤﹣﹣=﹣;….(1)、根据以上规律写出第⑥个等式: ;(2)、写出你猜想的第n个等式(用含n的式子表示),并说明猜想的正确性.22. 某商场准备购进甲、乙两种文具,若每个甲文具的进价比每个乙文具的进价少3元,且用200元购进甲文具的数量与用320元购进乙文具的数量相同.(1)、求每个甲文具和每个乙文具的进价分别是多少元?(2)、该商场购进甲、乙两种文具共90个,且购进甲文具的数量不低于乙文具的数量的3倍.若每个甲文具的售价为8元,每个乙文具的售价为12元,问该商场应怎样购进甲、乙两种文具才能使销售完这批文具时利润最大?最大利润是多少元?(利润=售价﹣进价)23. 已知AB∥CD,线段EF分别与AB,CD相交于点E,F.
(1)、和相等的角有;(2)、若 , 求的度数.19. 先化简,再求值:()÷ , 其中a为整数,且a满足2≤a<5.20. 已知关于x,y的方程组的解满足x≥0,y<0.(1)、求m的取值范围;(2)、在m的取值范围内,当m取何整数时,不等式(2m+1)x<2m+1的解集为x>1?21. 观察下列等式:①1﹣1﹣=﹣;②﹣﹣=﹣;③﹣﹣=﹣;④﹣﹣=﹣;⑤﹣﹣=﹣;….(1)、根据以上规律写出第⑥个等式: ;(2)、写出你猜想的第n个等式(用含n的式子表示),并说明猜想的正确性.22. 某商场准备购进甲、乙两种文具,若每个甲文具的进价比每个乙文具的进价少3元,且用200元购进甲文具的数量与用320元购进乙文具的数量相同.(1)、求每个甲文具和每个乙文具的进价分别是多少元?(2)、该商场购进甲、乙两种文具共90个,且购进甲文具的数量不低于乙文具的数量的3倍.若每个甲文具的售价为8元,每个乙文具的售价为12元,问该商场应怎样购进甲、乙两种文具才能使销售完这批文具时利润最大?最大利润是多少元?(利润=售价﹣进价)23. 已知AB∥CD,线段EF分别与AB,CD相交于点E,F. (1)、请在横线上填上合适的内容,完成下面的解答:
(1)、请在横线上填上合适的内容,完成下面的解答:如图1,当点P在线段EF上时,已知∠A=35°,∠C=62°,求∠APC的度数;
解:过点P作直线PH∥AB,
所以∠A=∠APH,依据是 ▲ ;
因为AB∥CD,PH∥AB,
所以PH∥CD,依据是 ▲ ;
所以∠C=( ),
所以∠APC=( ▲ )+( ▲ )=∠A+∠C=97°.
(2)、当点P,Q在线段EF上移动时(不包括E,F两点):①如图2,∠APQ+∠PQC=∠A+∠C+180°成立吗?请说明理由;
②如图3,∠APM=2∠MPQ,∠CQM=2∠MQP,∠M+∠MPQ+∠PQM=180°,请直接写出∠M,∠A与∠C的数量关系.