安徽省池州市贵池区2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 四个数0，- $\sqrt{2}$ ， 2021， $\frac{22}{7}$ 中，为无理数的是（）

A、0 B、2021 C、- $\sqrt{2}$ D、 $\frac{22}{7}$

查看试题解析
2. 下列等式正确的是（）

A、 $\sqrt{- 9} = - 3$ B、 $\sqrt{\frac{49}{144}} = \pm \frac{7}{12}$ C、 $\sqrt[3]{{(- 8)}^{2}} = 4$ D、 $- \sqrt[3]{- \frac{27}{8}} = - \frac{3}{2}$

查看试题解析
3. 下列计算结果是a⁵ 的是（）

A、a²+a³ B、a¹⁰÷a² C、（a²）³ D、a²·a³

查看试题解析
4. 某种冠状病毒的直径是120纳米，1纳米=10^-9米，则这种冠状病毒的直径是（）米．

A、1.2×10^-7 B、1.2×10^-8 C、12×10^-9 D、120×10^-10

查看试题解析
5. 下列各不等式中，能推出 a>b的是（）

A、a-3<b-3 B、-4a<-4b C、 $- \frac{3}{2}$ a> $- \frac{3}{2}$ b D、a²>b²

查看试题解析
6. 如图（1），从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后将剩余的部分剪拼成一个长方形，如图（2），通过计算阴影部分的面积可以得到（）

A、（a-2b）²=a²-4ab+b² B、（a+2b）²=a²+4ab+b² C、（a-2b）（a+2b）=a²-4b² D、（a+b）²=a²+2ab+b²

查看试题解析
7. 若把 $x$ ， $y$ 的值同时扩大为原来的2倍，则下列分式的值保持不变的是（）

A、 $\frac{{(x + y)}^{2}}{x^{2}}$ B、 $\frac{x y}{x + y}$ C、 $\frac{x + 2}{y + 2}$ D、 $\frac{x - 2}{y - 2}$

查看试题解析
8. 下列说法正确的个数是（）
①同位角相等； ②同旁内角互补，两直线平行；③若a//b，b//c，则a//c；④直线外一点到这条直线的距离是指这一点到这条直线的垂线段；⑤在连接直线外一点与直线上各点的线段中，垂线段最短；⑥平移既改变图形的位置，也改变图形的形状与大小．

A、2个 B、3个 C、4个 D、5个

查看试题解析
9. 如图，给出下列条件：①∠1＝∠2：②∠3＝∠4：③AB∥CE，且∠ADC＝∠B：④AB∥CE，且∠BCD＝∠BAD.其中能推出BC∥AD的条件为（）

A、①② B、②④ C、②③ D、②③④

查看试题解析
10. 某校举行“停课不停学，名师陪你在家学”活动，计划投资8000元建设几间直播教室，为了保证教学质量，实际每间建设费用增加了20%，并比原计划多建设了一间直播教室，总投资追加了4000元.根据题意，求出原计划每间直播教室的建设费用是（）

A、1600元 B、1800元 C、2000元 D、2400元

查看试题解析

二、填空题

11. 分解因式： $m a^{2} - 4 m a b + 4 m b^{2} =$ ．

查看试题解析
12. 已知整数x满足- $\sqrt{2}$ <x< $\sqrt{3}$ -2，则整数x的值为．

查看试题解析
13. 当x的值是时，分式 $\frac{| x | - 3}{2 x - 6}$ 的值为零．

查看试题解析
14. 若 $a - b = 2 ， a b = 1$ ，则 $a^{2} + b^{2} =$ ．

查看试题解析
15. 已知关于x的不等式组 ${\begin{array}{l} \frac{x - m}{2} \geq 2 \\ x - 4 \geq 3 (x - 4) \end{array}$ 的最小整数解是2，则实数m的取值范围是．

查看试题解析
16. 如图，直线AB、CD相交于点O，OF⊥CD，∠DOE∶∠BOD=3∶2，若∠AOC=28°，则∠EOF的度数为．

查看试题解析
17. 当m＝时，解关于x的分式方程 $\frac{2}{x + 1} + \frac{5}{1 - x} = \frac{m}{x^{2} - 1}$ 会产生增根．

查看试题解析
18. 如果角α和角β的两边分别平行，且满足2α＝β+60°，则角α的度数是.

查看试题解析
19. 关于x的方程 $\frac{3 x}{x - 3} - 1 = \frac{m}{3 - x}$ 的解不小于1，则 m 的取值范围为．

查看试题解析
20. 在“新冠肺炎”这场没有硝烟的战争中，各行各业都涌现出了一批“最美逆行者”，其中抗疫最前沿的就是护士。某医院护安排护士若干名负责护理新冠病人，每名护士护理4名新冠病人，有20名新冠病人没人护理，如果每名护士护理8名新冠病人，有一名护士护理的新冠病人多于1人不足8人，这个医院安排了名护士护理新冠病人。

查看试题解析

三、解答题

21.

(1)、计算∶（-1）²⁰²¹+（ $π$ +5）⁰- $\sqrt{4}$ +（- $\frac{1}{2}$ ）^-2

(2)、先化简，再求值∶（2- $\frac{4}{x + 3}$ ）÷ $\frac{x^{2} - 1}{x^{2} + 6 x + 9}$ ，其中x= -2．

查看试题解析
22. 解不等式组与方程∶

(1)、解不等式组 ${\begin{array}{l} 3 (x - 2) \geq 4 - 2 x (1) \\ 2 + 2 x < 3 x + 3 (2) \end{array}$ 并把解集表示在数轴上．

(2)、解方程∶ $\frac{x + 1}{x + 3} - \frac{12}{x^{2} - 9} = 1$

查看试题解析
23. 如图，是一道例题及部分解答过程，其中A、B是两个关于x，y的二项式．
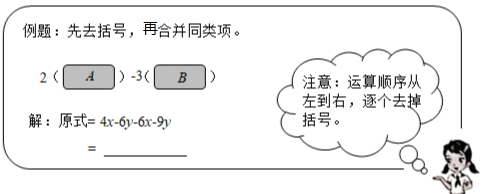
请仔细观察上面的例题及解答过程，完成下列问题∶

(1)、直接写出多项式A和 B，并求出该例题的运算结果；

(2)、求多项式A与B的平方差．

查看试题解析
24. 观察下列方程，回答问题
① $\frac{1}{x + 1} + 1 = \frac{2}{x + 1}$ 的解为x=0
② $\frac{2}{x + 1} + 1 = \frac{4}{x + 1}$ 的解为x=1
③ $\frac{3}{x + 1} + 1 = \frac{6}{x + 1}$ 的解为x=2
④ $\frac{4}{x + 1} + 1 = \frac{8}{x + 1}$ 的解为 x=3

(1)、请直接写出第⑤个方程及它的解；

(2)、请你写出第 n（n为正整数）个方程，并求出它的解．（写出解答过程）

查看试题解析
25. 如图，∠ENC+∠CMG=180°，AB//CD．

(1)、请判断∠2 与∠3 是否相等，请说明理由．

(2)、若∠A=∠1+70°，∠ACB=42°，求∠B的度数．

查看试题解析
26. 甲、乙两支工程队修建公路，已知甲队每天修路的长度比乙队每天修路的长度多 50 米，甲队修路 600米与乙队修路 300米用的天数相同．

(1)、求甲、乙两支工程队每天各修路多少米？

(2)、计划修建长度为3600米的公路，因工程需要，甲、乙两支工程队都要参与这条公路的修建，若甲队每天所需费用为1.2 万元，乙队每天所需费用为0.5 万元，在总费用不超过 40 万元的情况下，至少安排乙队施工几天？

查看试题解析