安徽省安庆市太湖县2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-06-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列说法正确的是（）

A、－4的平方根是－2 B、－8的立方根是±2 C、负数没有立方根 D、－1的立方根是－1

查看试题解析
2. 满足- $\sqrt{2}$ <x< $\sqrt{3}$ 的整数共有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
3. 下列不等式变形正确的是 $()$

A、由 $a > b$ ，得 $a c > b c$ B、由 $a > b$ ，得 $- 2 + a < b - 2$ C、由 $- \frac{1}{2} > - 1$ ，得 $- \frac{a}{2} > - a$ D、由 $a > b$ ，得 $c - a < c - b$

查看试题解析
4. 中国抗疫取得了巨大成就，堪称奇迹，为世界各国防控疫情提供了重要借鉴和支持，让中国人民倍感自豪.2020年1月12日，世界卫生组织正式将2019新型冠状病毒名为 $2019 - n C o V$ ．该病毒的直径在0.00000008米-0.000000012米，将0.000000012用科学记数法表示为 $a \times 1 0^{n}$ 的形式，则 $n$ 为（）．

A、 $- 8$ B、 $- 7$ C、7 D、8

查看试题解析
5. 下列分解因式中，①x²+2xy+x=x（x+2y）；②x²+4x+4=（x+2）²；③﹣x²+y²=（x+y）（x﹣y）．正确的个数为（）

A、3 B、2 C、1 D、0

查看试题解析
6. 若关于x的分式方程 $\frac{3 x}{x - 2}$ ＝ $\frac{m}{2 - x}$ +5的解为正数，则m的取值范围为（）

A、m＜﹣10 B、m≤﹣10 C、m≥﹣10且m≠﹣6 D、m＞﹣10且m≠﹣6

查看试题解析
7. 若关于x、y的二元一次方程组 $\{\begin{matrix} 3 x + y = 1 + a \\ x + 3 y = 3 \end{matrix}$ 的解满足x＋y<2，则a的取值范围为 ( )

A、a<4 B、a>4 C、a<－4 D、a>－4

查看试题解析
8. 计算 ${(\frac{5}{7})}^{2021} \times {(\frac{7}{5})}^{2020} \times (- 1)^{2023}$ 的结果是（）

A、 $\frac{5}{7}$ B、 $\frac{7}{5}$ C、 $- \frac{5}{7}$ D、 $- \frac{7}{5}$

查看试题解析
9. 图（1）是一个长为2a，宽为 $2 b (a > b)$ 的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小完全相同的小长方形，然后按图（2）那样拼成一个正方形，则中间空余的部分的面积是（）

A、ab B、 $(a + b)^{2}$ C、 $(a - b)^{2}$ D、 $a^{2} - b^{2}$

查看试题解析
10. 在2020年3月底新过师炎疫情在我国得到快速控制，教育部要求低风险区错时、错峰开学，某校在只有初三年级开学时，一段时间用掉120瓶消毒液，在初二、初一年级也错时、错峰开学后，平均每天比原来多用4瓶消毒液，这样120瓶消毒液比原来少用5天，若设原来平均每天用掉x瓶消毒液，则可列方程是（）

A、 $\frac{120}{x} - 5 = \frac{120}{x + 4}$ B、 $\frac{120}{x - 4} - 5 = \frac{120}{x}$ C、 $\frac{120}{x} + 5 = \frac{120}{x + 4}$ D、 $\frac{120}{x - 4} + 5 = \frac{120}{x}$

查看试题解析

二、填空题

11. 已知 $x^{2} + y^{2} = 25 ， x + y = 7 ，$ 则 $x - y =$ .

查看试题解析
12. 定义a※b=a（b+1），例如2※3=2×（3+1）=2×4=8．则（x﹣1）※x的结果为．

查看试题解析
13. 商家花费760元购进某种水果80千克，销售中有5%的水果正常损耗，为了避免亏本，售价至少应定为元/千克

查看试题解析
14. 如图，已知AB，CD，EF互相平行，且∠ABE＝70°，∠ECD＝150°，则∠BEC＝°.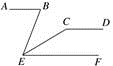

查看试题解析

三、解答题

15. 计算： $| - 3 | + (π - 3)^{0} - \sqrt[3]{- 64} \div 2 - 4 \times 2^{- 1}$ ．

查看试题解析
16. 观察下列等式：①3²﹣1²=8×1；②5²﹣3²=8×2；③7²﹣5²=8×3；④9²﹣7²=8×4

(1)、请你紧接着写出两个等式：⑤；⑥；

(2)、根据以上式子的规律，请你写出第n个式子；

(3)、利用这个规律计算：2021²﹣2019²的值．

查看试题解析
17. 已知a为大于2的整数，若关于x的不等式组 ${\begin{array}{l} 2 x - a \leq 0 \\ x \geq 2 \end{array}$ 无解．

(1)、求a的值．

(2)、化简并求值： $(\frac{a^{2} - 2}{a} - 1) + \frac{a - 2}{a}$ ．

查看试题解析
18. 网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC平移，使点A平移至点A'．

(1)、画出平移后的△A'B'C'（点B'、C'分别是B、C的对应点）；

(2)、△A'B'C'的面积为；

(3)、若连接AA'、CC'，则这两条线段之间的关系是．

查看试题解析
19. 如图，CD∥AB，∠DCB=70°，∠CBF=20°，∠EFB=130°，

(1)、问直线EF与AB有怎样的位置关系？加以证明；

(2)、若∠CEF=70°，求∠ACB的度数．

查看试题解析
20. 书是人类进步的阶梯！为爱护书一般都将书本用封皮包好，现有一本如图1的数学课本，其长为26cm、宽为18.5cm、厚为1cm，小海宝用一张长方形纸包好了这本数学书，他将封面和封底各折进去xcm封皮展开后如图（2）所示，求：

(1)、则小海宝所用包书纸的面积是多少？（用含x的代数式表示）

(2)、当封面和封底各折进去2cm时，请帮小海宝计算一下他需要的包装纸至少需要多少平方厘米？

查看试题解析
21. 华联商场预测某品牌村衫能畅销市场，先用了8万元购入这种衬衫，面市后果然供不应求，于是商场又用了17.6万元购入第二批这种衬衫，所购数量是第一批购入量的2倍，但单价贵了4元.商场销售这种衬衫时每件定价都是58元，最后剩下的150件按定价的八折销售，很快售完.

(1)、第一次购买这种衬衫的单价是多少？

(2)、在这两笔生意中，华联商场共赢利多少元？

查看试题解析
22. 问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°．求∠APC度数．小明的思路是：如图2，过点P作PE∥AB，通过平行线性质，可得∠APC=50°+60°=110°．

(1)、问题迁移：
如图3．AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β．猜想∠CPD、∠α、∠β之间有何数量关系？请说明理由：

(2)、在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请写出∠CPD、∠a、∠β之间的数量关系，选择其中一种情况画图并证明．

查看试题解析
23. 【知识回顾】
七年级学习代数式求值时，遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关，求a的值”，通常的解题方法是：把x、y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含x项的系数为0，即原式＝（a+3）x﹣6y+5，所以a+3＝0，则a＝﹣3．

(1)、【理解应用】
若关于x的多项式（2x﹣3）m+2m²﹣3x的值与x的取值无关，求m值；

(2)、已知A＝（2x+1）（x﹣1）﹣x（1﹣3y），B＝﹣x²+xy﹣1，且3A+6B的值与x无关，求y的值；

(3)、【能力提升】
7张如图1的小长方形，长为a，宽为b，按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分（图中阴影部分），设右上角的面积为S₁ ，左下角的面积为S₂ ，当AB的长变化时，S₁﹣S₂的值始终保持不变，求a与b的等量关系．

查看试题解析