安徽省安庆市2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-06-29 类型:期末考试
一、单选题
-
1. 在四个数π、、0、-1中,是无理数的( )A、π B、 C、0 D、-12. 下列运算中,正确的是( )A、 B、 C、 D、3. 如图所示是番茄果肉细胞结构图,番茄果肉细胞的直径约为0.0006米,将0.0006用科学记数法表示为( )
 A、 B、 C、 D、4. 若a>b,则下列不等式变形不一定成立的是( )A、a-1>b-1 B、ac2>bc2 C、-a<-b D、 >5. 下列各式中,因式分解正确的是( )A、 B、 C、 D、6. 下列各组图形,可以经过平移变换由一个图形得到另一个图形的是( )A、
A、 B、 C、 D、4. 若a>b,则下列不等式变形不一定成立的是( )A、a-1>b-1 B、ac2>bc2 C、-a<-b D、 >5. 下列各式中,因式分解正确的是( )A、 B、 C、 D、6. 下列各组图形,可以经过平移变换由一个图形得到另一个图形的是( )A、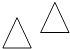 B、
B、 C、
C、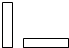 D、
D、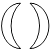 7. 如图,已知 , 如果 , 那么的度数为( )
7. 如图,已知 , 如果 , 那么的度数为( )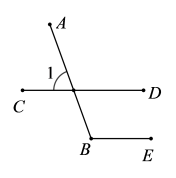 A、60° B、100° C、110° D、120°8. 若x2+(m-3)x+16是完全平方式,则m的值是( )A、-5 B、11 C、-5或11 D、-11或59. 若 , 则n的值为( )A、0 B、1 C、2 D、310. 如图,直线 , 点A在直线m上,BC在直线n上,构成△ABC,把△ABC向右平移BC长度的一半得到△A´B´C´(如图①),再把△向右平移BC长度的一半得到△(如图②),再继续上述的平移得到图③,…,通过观察可知图①中有4个三角形,图②中有8个三角形,则第2021个图形中三角形的个数是( )
A、60° B、100° C、110° D、120°8. 若x2+(m-3)x+16是完全平方式,则m的值是( )A、-5 B、11 C、-5或11 D、-11或59. 若 , 则n的值为( )A、0 B、1 C、2 D、310. 如图,直线 , 点A在直线m上,BC在直线n上,构成△ABC,把△ABC向右平移BC长度的一半得到△A´B´C´(如图①),再把△向右平移BC长度的一半得到△(如图②),再继续上述的平移得到图③,…,通过观察可知图①中有4个三角形,图②中有8个三角形,则第2021个图形中三角形的个数是( )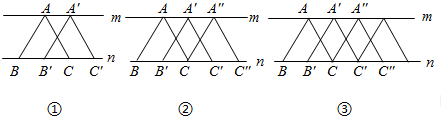 A、4042 B、6063 C、8084 D、8088
A、4042 B、6063 C、8084 D、8088二、填空题
-
11. 若分式 有意义,则x的取值范围是 .12. 将一副三角板(∠A=30°,∠E=45°)按如图方式摆放,使得AB//EF,则∠AOF= .
 13. 如图,直线AB//CD,点M、N分别在直线AB、CD上,点E为直线AB与CD之间的一点,连接ME、NE,且∠MEN=80°,∠AME的角平分线与∠CNE的角平分线交于点F,则∠MFN的度数为 .
13. 如图,直线AB//CD,点M、N分别在直线AB、CD上,点E为直线AB与CD之间的一点,连接ME、NE,且∠MEN=80°,∠AME的角平分线与∠CNE的角平分线交于点F,则∠MFN的度数为 .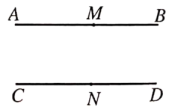 14. 定义运算 , 下列给出了关于这种运算的几个结论:(1);(2)是无理数;(3)方程不是二元一次方程;(4)不等式组的解集是 . 其中正确的是(填序号).
14. 定义运算 , 下列给出了关于这种运算的几个结论:(1);(2)是无理数;(3)方程不是二元一次方程;(4)不等式组的解集是 . 其中正确的是(填序号).三、解答题
-
15. 计算:16. 解不等式组 , 并将解集在数轴上表示出来.
 17. 计算:18. 解方程: = +119. 如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形的顶点都在正方形网格的格点上,将三角形ABC向上平移个单位,再向右平移个单位,平移后得到三角形 , 其中图中直线上的点是点的对应点.
17. 计算:18. 解方程: = +119. 如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形的顶点都在正方形网格的格点上,将三角形ABC向上平移个单位,再向右平移个单位,平移后得到三角形 , 其中图中直线上的点是点的对应点. (1)、画出平移后得到的三角形;(2)、m-n=;(3)、在直线上存在一点 , 使所围成的四边形的面积为6,请在直线上画出所有符合要求的格点 .20. 先化简,再求值: , 其中满足 .21. 某市启动“城市公园”建设,计划对面积为3600m2的区域进行绿化,经投标由甲、乙两个工程队来完成,已知甲工程队完成绿化360m2的面积与乙工程队完成绿化240m2的面积所用时间相同,若甲工程队每天比乙工程队多完成绿化30m2 ,(1)、求甲、乙两工程队每天各能完成多少面积的绿化?(2)、若甲队每天绿化费用是1.2万元,乙队每天绿化费用是0.5万元,要使这次绿化的总费用不超过45万元,则至少应安排乙工程队绿化多少天?
(1)、画出平移后得到的三角形;(2)、m-n=;(3)、在直线上存在一点 , 使所围成的四边形的面积为6,请在直线上画出所有符合要求的格点 .20. 先化简,再求值: , 其中满足 .21. 某市启动“城市公园”建设,计划对面积为3600m2的区域进行绿化,经投标由甲、乙两个工程队来完成,已知甲工程队完成绿化360m2的面积与乙工程队完成绿化240m2的面积所用时间相同,若甲工程队每天比乙工程队多完成绿化30m2 ,(1)、求甲、乙两工程队每天各能完成多少面积的绿化?(2)、若甲队每天绿化费用是1.2万元,乙队每天绿化费用是0.5万元,要使这次绿化的总费用不超过45万元,则至少应安排乙工程队绿化多少天?
