江苏省泰州市海陵区五校2021-2022学年七年级下学期期末考试数学试卷

试卷更新日期：2022-06-28 类型：期末考试

进入出卷网下载

一、选择题（本大题共6小题，每小题3分，共18分）

1. 如图，A，B，C，D中的哪幅图案可以通过图案①平移得到（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、b²•b³＝b⁶ B、（a²）³＝a⁶ C、﹣a²÷a＝a D、（a³）²•a＝a⁶

查看试题解析
3. 下列命题中，假命题是（）

A、对顶角相等 B、不相等的两个角不是对顶角 C、两直线平行，内错角相等 D、同旁内角互补

查看试题解析
4. 下列长度的三根木棒首尾相接，不能做成三角形框架的是( )

A、5cm、7cm、2cm B、7cm、13cm、10cm C、5cm、7cm、11cm D、5cm、10cm、13cm

查看试题解析
5. 如图，a∥b，M、N分别在a，b上，P为两平行线间一点，那么，∠1+∠2+∠3＝（）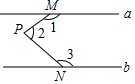

A、180° B、270° C、360° D、540°

查看试题解析
6. 关于x的不等式 ${\begin{array}{l} x - m > 0 \\ 7 - 2 x > 1 \end{array}$ 的整数解只有4个，则m的取值范围是（）

A、﹣2＜m≤﹣1 B、﹣2≤m≤﹣1 C、﹣2≤m＜﹣1 D、﹣3＜m≤﹣2

查看试题解析

二、填空题（本大题共10小题，每小题3分，共30分）

7. 在芯片上某种电子元件大约只占0.000 000 0356 mm² ，这个数用科学记数法表示为mm² ．

查看试题解析
8. 命题“直角三角形的两个锐角互余”的逆命题为．

查看试题解析
9. 一个n边形的内角和是1080°，那么n= ．

查看试题解析
10. 已知x、y满足方程组 ${\begin{array}{l} x + 2 y = - 2 \\ 2 x + y = 5 \end{array}$ ，则x+y的值为．

查看试题解析
11. 如图，将分别含有 $30 °$ 、 $45 °$ 角的一副三角板重叠，使直角顶点重合，若两直角重叠形成的角为 $65 °$ ，则图中角 $α$ 的度数为.

查看试题解析
12. 如图，已知在△ABD和△ABC中，∠DAB＝∠CAB，点A、B、E在同一条直线上，若可根据“SAS”判断△ABD≌△ABC；则还需添加的一个条件是．

查看试题解析
13. 若3^x=4，3^y=5，则3^x-2y的值为．

查看试题解析
14. 如图，在△ABC中，沿DE折叠，点A落在三角形所在的平面内的点为A^，，若∠A=30°，∠BDA^，=86°，则∠CEA^，的度数为．

查看试题解析
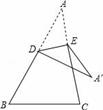15. 若关于x的不等式组 ${\begin{array}{l} 3 x - a > 0 \\ 4 - 2 x > 0 \end{array}$ 无解，则a的取值范围为．

查看试题解析
16. 如图，在正方形方格中，各正方形的顶点叫做格点，三个顶点都在格点上的三角形称为格点三角形。图中 $△ A B C$ 是格点三角形，请你找出方格中所有与 $△ A B C$ 全等，且以A为顶点的格点三角形．这样的三角形共有个（ $△ A B C$ 除外）．

查看试题解析

三、解答题（本大题共10小题，共102分）

17. 计算：

(1)、（π﹣2022）⁰﹣（﹣ $\frac{1}{2}$ ）^-2

(2)、(x-2y)(2y+x)-(2x-y)²

查看试题解析
18. 把下列各式因式分解：

(1)、x ² – 25

(2)、-4x²+24x-36

查看试题解析
19. 解下列方程组：

(1)、 ${\begin{array}{l} 2 x + y = 1 \\ 3 x - 2 y = 5 \end{array}$

(2)、 ${\begin{array}{l} \frac{x}{3} - \frac{y}{2} = 1 \\ 3 x - 5 y = 10 \end{array}$

查看试题解析
20. 解不等式组

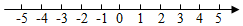(1)、解不等式组，并在数轴上表示不等式的解集： ${\begin{cases} 2 x \leq 6 - x \\ 3 x - 1 < 5 (x + 1) \end{cases}$

(2)、解不等式组 ${\begin{array}{l} 2 (x - 2) \leq 2 - x \\ \frac{x + 4}{3} < \frac{x + 3}{2} \end{array}$ ，并写出它的整数解．

查看试题解析
21. 已知关于x、y的方程组 ${\begin{array}{l} x + 2 y = 4 a + 3 \\ 3 x - 2 y = 1 \end{array}$ 的解满足x是正数，y是非负数，求a 的取值范围．

查看试题解析
22. 如图，直线 $E F$ 分别与直线 $A B$ ， $C D$ 交于点E，F. $E M$ 平分 $∠ B E F$ ， $F N$ 平分 $∠ C F E$ ，且 $E M$ ∥ $F N$ .求证： $A B$ ∥ $C D$ .

查看试题解析
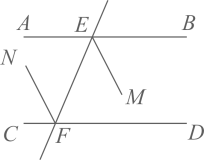23. 如图，在△ABC中，∠ACB＝90°，点E在AC的延长线上，ED⊥AB于点D，BC、DE交于O，BC＝ED．

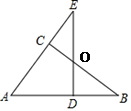(1)、求证：∠B=∠E

(2)、求证：OE＝OB．

查看试题解析
24. 某校计划为教师购买甲、乙两种词典.已知购买1本甲种词典和2本乙种词典共需170元，购买2本甲种词典和3本乙种词典共需290元.

(1)、求每本甲种词典和每本乙种词典的价格分别为多少元？

(2)、学校计划购买甲种词典和乙种词典共30本，总费用不超过1600元，那么最多可购买甲种词典多少本？

查看试题解析
25. 直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B在射线OM上运动．

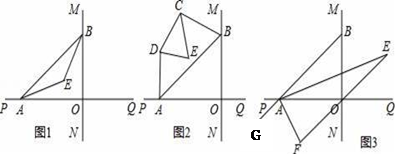(1)、如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．

(2)、如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．

(3)、如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有两个角度数的比是3：2，请直接写出∠ABO的度数．

查看试题解析
26. 如图，∠MON=90°，点A、B分别在射线OM、ON上，点C在∠MON内部．

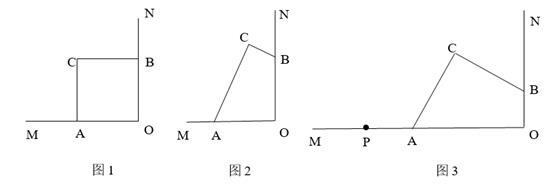(1)、若OA=OB，
①如图1，若CA⊥OM，CB⊥ON．求证：CA=CB．

②如图2，若∠ACB=90°．求证：OC平分∠ACB．

(2)、如图3，点A、B分别在射线OM、ON上运动，点C随之运动，且∠ACB=90°，AC=BC．P为OM上一定点，当点C运动到何处时，PC的长度最短？
请用尺规作图作出PC最短时C点的位置（保留作图痕迹，不要写作法），并请简要说明理由．

查看试题解析