江苏省南京市联合体2021-2022学年八年级下学期期末考试数学试卷

试卷更新日期：2022-06-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若式子 $\sqrt{x - 4}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x > 4$ B、 $x < 4$ C、 $x \geq 4$ D、 $x \leq 4$

查看试题解析
3. 下列事件是随机事件的是（）

A、抛出的篮球会下落 B、没有水分，种子发芽 C、购买一张彩票会中奖 D、自然状态下，水会往低处流

查看试题解析
4. 分式 $\frac{1}{6 x^{2}}$ 与 $- \frac{1}{3 x y}$ 的最简公分母是（）

A、 $6 x^{3} y$ B、 $6 x^{2} y$ C、 $18 x^{2} y$ D、 $18 x^{3} y$

查看试题解析
5. 如图，一次函数 $y_{1} = k x + b$ 与反比例函数 $y_{2} = \frac{m}{x}$ 的图象相交于 $A (a ， 2)$ 和 $B (- 4 ， - 3)$ ，则不等式 $\frac{m}{x} > k x + b$ 的解集是（）

A、 $x < - 4$ 或 $0 < x < 6$ B、 $x < - 3$ 或 $0 < x < 6$ C、 $- 3 < x < 0$ 或 $x > 6$ D、 $- 4 < x < 0$ 或 $0 > x$

查看试题解析
6. 如图，在正方形ABCD中， $A B = 4$ ， E为AB边上一点，点F在BC边上，且 $B F = 1$ ，将点E绕着点F顺时针旋转90°得到点G，连接DG，则DG的长的最小值为（）

A、2 B、 $2 \sqrt{2}$ C、3 D、 $\sqrt{10}$

查看试题解析

二、填空题

7. 计算： ${(\sqrt{2})}^{2} =$ ； $\sqrt{{(- 2)}^{2}} =$ .

查看试题解析
8. 小明同一条件下进行射门训练，结果如下表：
射门次数n
20
50
100
200
500
踢进球门频数m
13
35
58
104
255
踢进球门频率 $\frac{m}{n}$
0.65
0.70
0.58
0.52
0.52
根据表中数据，估计小明射门一次进球的概率为.（精确到0.1）

查看试题解析
9. 比较大小： $\frac{\sqrt{5} - 1}{2}$ $\frac{1}{2}$ （填“＞”“＜”“＝”）.

查看试题解析
10. 为了解某校500名初二学生每天做课后作业的时间，从中抽取50名学生进行调查，该调查中的样本容量是.

查看试题解析
11. 已知平行四边形ABCD中，∠A+∠C=110°，则∠B的度数为．

查看试题解析
12. 已知A（x₁ ， y₁）B（x₂ ， y₂）为反比例函数 $y=- \frac{3}{x}$ 图象上的两点，且x₁＜x₂＜0，则：y₁y₂（填“＞”或“＜”）．

查看试题解析
13. 若分式方程 $\frac{1}{x - 3} = \frac{a - x}{x - 3}$ 有增根，则a的值是.

查看试题解析
14. 反比例函数 $y = \frac{k}{x}$ 的图象过点 $(- 2 ， a)$ 、 $(2 ， b)$ ，则 $a + b =$ .

查看试题解析
15. 如图，平行四边形ABCD的对角线AC、BD相交于点O，E、F分别是AO、BO的中点.若 $A C + B D = 24$ cm， $△ O A B$ 的周长是18cm，则 $E F =$ cm.

查看试题解析
16. 如图，B、C分别是反比例函数 $y = \frac{6}{x} (x > 0)$ 与 $y = - \frac{2}{x} (x > 0)$ 的图象上的点，且 $B C ∥ y$ 轴，过点C作BC的垂线交于y轴于点A，则 $△ A B C$ 的面积为.

查看试题解析

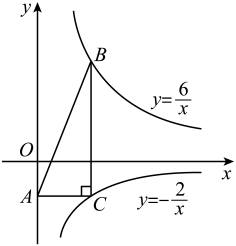
三、解答题

17. 计算：

(1)、 $\sqrt{12} - 2 \sqrt{\frac{1}{3}}$ ；

(2)、 $(2 \sqrt{5} + 3 \sqrt{2}) (2 \sqrt{5} - 3 \sqrt{2})$

查看试题解析
18. 计算

(1)、 $\frac{2 a - b}{a + b} + \frac{a + 4 b}{a + b}$ ；

(2)、 $(a - 1) \cdot \frac{3}{a^{2} + a} \div \frac{a - 1}{a}$

查看试题解析
19. 先化简，再求值： $(1 - \frac{2}{x + 1}) \div \frac{x^{2} - 2 x + 1}{x + 1}$ ，其中 $x = \sqrt{3} + 1$ .

查看试题解析
20. 解方程： $\frac{x}{x - 1} + \frac{3}{1 - x} = 2$ .

查看试题解析

21. 八（1）班学生参加了学校举行的“冬奥知识竞赛”活动，赛后老师对成绩进行分析，制作如下的频数分布表和扇形统计图：

八（1）班学生冬奥知识竞赛成绩频数表

类别	分数段	频数（人数）
A	60≤x＜70	a
B	70≤x＜80	16
C	80≤x＜90	24
D	90≤x＜100	6

请根据以上统计图表解答下列问题：

(1)、八（1）班总数为；

(2)、

a =

；

(3)、扇形统计图中，类别B所在扇形的圆心角度数是°.

(4)、全校共有720名学生参加比赛，若成绩在80分以上（含80分）为优秀，估计该校成绩优秀的学生有多少名？

查看试题解析

22. 如图，菱形ABCD的对角线相交于O点，DE $∥$ AC，CE $∥$ BD.

(1)、求证：四边形OCED是矩形；

(2)、若AD =5，BD =8，计算DE的值.

查看试题解析
23. 某司机驾驶汽车从甲地去乙地，他以 $80 k m / h$ 的平均速度用 $6 h$ 到达目的地.

(1)、当他按原路匀速返回时，汽车的速度v与时间t有怎样的函数关系？

(2)、如果该司机返回到甲地的时间不超过 $5 h$ ，那么返程时的平均速度不能小于多少？

查看试题解析
24. 常态化疫情防控以来，某社区核酸检测点数量由去年的2个增加到今年的6个，假设每个检测点的工作效率相同，该社区今年检测1200人的时间相比去年节省了2小时.求该社区一个检测点每小时可检测多少人？

查看试题解析
25. 在四边形ABCD中，E、F、G、H分别是AD、AB、BC、CD边上的点，则称四边形EFGH为四边形ABCD的内接四边形.

(1)、如图①，在平行四边形ABCD中，AC、BD交于点O，四边形EFGH为▱ABCD的内接四边形，对角线EG、FH都经过点O.求证：四边形EFGH为平行四边形；

(2)、如图②，用无刻度的直尺和圆规在平行四边形ABCD中作出对角线最短的内接矩形EFGH；（不写作法，保留作图痕迹）

(3)、如图③，在矩形ABCD中， $A B = 4$ ， $B C = 6$ ，若四边形EFGH为矩形ABCD的内接菱形，则AE的取值范围是.

查看试题解析
26. 在矩形ABCD中，P是线段BC上的一个动点，将△ABP沿直线AP翻折，点B的对应点为E，直线PE与直线AD交于点F.

(1)、如图①，当点F在AD的延长线上时，求证 $A F = P F$ ；

(2)、若 $A B = 6$ ， BC足够长，当点E到直线AD的距离等于3时，求BP的长；

(3)、若 $A B = 6$ ， $B C = 10$ .当点P、E、D在同一直线上（如图②）时，点P开始向点C运动，到与C重合时停止，则点F运动的路程是.

查看试题解析

射门次数n	20	50	100	200	500
踢进球门频数m	13	35	58	104	255
踢进球门频率 $\frac{m}{n}$	0.65	0.70	0.58	0.52	0.52