福建省福州市台江区2021-2022学年八年级下学期期末考试数学试卷
试卷更新日期:2022-06-28 类型:期末考试
一、单选题
-
1. 二次根式有意义的条件是( )A、x>3 B、x<3 C、x≥3 D、x≤32. 下列各组数中能作为直角三角形的三边长的是( )A、1,2,3 B、3,4,5 C、4,5,6 D、7,8,93. 下列计算正确的是( )A、 B、 C、 D、4. 把直线y=3x向下平移2个单位,得到的直线是( )A、y=3x﹣2 B、y=3(x﹣2) C、y=3x+2 D、y=3(x+2)5. 在“我的中国梦”演讲比赛中,有5名学生参加决赛,他们决赛的最终成绩各不相同,其中一名学生想要知道自己能否进入前3名,不仅要了解自己的成绩,还要了解5名学生成绩的( )A、中位数 B、众数 C、平均数 D、方差6. 在边长为1的小正方形组成的网格中,A,B,C,D、E在格点上,长度是的线段是( )
 A、AB B、AC C、AD D、AE7. 如图,在中, , , 则的度数是( )
A、AB B、AC C、AD D、AE7. 如图,在中, , , 则的度数是( ) A、40° B、50° C、60° D、70°8. 已知点A(﹣2,m)和点B(3,n)都在直线y=2x+b的图象上,则m与n的大小关系为( )A、m>n B、m<n C、m≤n D、m≥n9. 要组织一次篮球联赛,赛制为单循环形式,每两队之间都赛一场,计划安排15场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )A、 x(x﹣1)=15 B、 x(x+1)=15 C、x(x+1)=15 D、x(x﹣1)=1510. 如图,正方形ABCD中,点E,F分别在CD,BC上,且AF⊥BE,垂足为G,则下列结论①BE=AF;②∠AFB+∠BEC=90°;③∠DAF=∠ABE;④BF=CE.其中正确的个数是( )
A、40° B、50° C、60° D、70°8. 已知点A(﹣2,m)和点B(3,n)都在直线y=2x+b的图象上,则m与n的大小关系为( )A、m>n B、m<n C、m≤n D、m≥n9. 要组织一次篮球联赛,赛制为单循环形式,每两队之间都赛一场,计划安排15场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )A、 x(x﹣1)=15 B、 x(x+1)=15 C、x(x+1)=15 D、x(x﹣1)=1510. 如图,正方形ABCD中,点E,F分别在CD,BC上,且AF⊥BE,垂足为G,则下列结论①BE=AF;②∠AFB+∠BEC=90°;③∠DAF=∠ABE;④BF=CE.其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
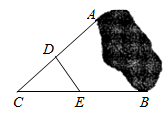
11. 若关于的方程的一个根是–1,则的值是.12. 函数(k是常数,)的图象上有两个点 , , 当时, , 写出一个满足条件的函数解析式: .13. 如图, , 两点被池塘隔开,在 外选一点 ,连接 和 .分别取 , 的中点 , ,测得 , 两点间的距离为 ,则 、 两点间的距离为 .
 14. 直线与直线在同一平面直角坐标系中的图象如图所示,则关于x的不等式的解集为.
14. 直线与直线在同一平面直角坐标系中的图象如图所示,则关于x的不等式的解集为. 15. 评定学生的学科期末成绩由考试分数,作业分数,课堂参与分数三部分组成,并按3:2:5的比例确定,已知小明的数学考试85分,作业90分,课堂参与80分,则他的数学期末成绩为分.16. 正方形ABCD中,AB=4,P是AC上一点,过点P作PM⊥AB于M,PN⊥BC于N.则MN最小值.
15. 评定学生的学科期末成绩由考试分数,作业分数,课堂参与分数三部分组成,并按3:2:5的比例确定,已知小明的数学考试85分,作业90分,课堂参与80分,则他的数学期末成绩为分.16. 正方形ABCD中,AB=4,P是AC上一点,过点P作PM⊥AB于M,PN⊥BC于N.则MN最小值.
三、解答题
-
17. 计算:(1)、;(2)、 .18. 解下列方程:(1)、;(2)、.19. 已知一次函数的图象经过点与.(1)、求这个一次函数的解析式;(2)、判断点是否在这个一次函数的图象上;(3)、直接写出关于x的一元一次方程kx+b=0的解.20. 两年前,生产1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元.随着生产技术的进步,现在生产1吨甲种药品的成本是3200元,生产1吨乙种药品的成本是3375元,哪种药品成本的年平均下降率较大?21. 某校抽取20名学生进行了每周课外阅读时间的调查,数据如下(单位:min):60,81,120,140,70,81,10,20,100,81,30,60,81,50,40,110,130,146,90,100.
【整理数据】按如表分段整理样本数据:
课外阅读时间x(min)
人数
3
5
8
a
【分析数据】样本数据的平均数、中位数、众数如表所示:
平均数
中位数
众数
80
b
c
根据以上信息,解答下列问题:
(1)、表格中的a= , b= , c=;(2)、如果该校八年级现有学生500人,根据抽样调查数据,估计每周用于课外阅读时间不少于80min的学生有多少名?22. 如图,中,是中线. (1)、过点C作 , 垂足为E;(尺规作图,保留作图痕迹,不写作法)(2)、当时,求的长.23. 某水果商从外地购进某种水果若干箱,需要租赁货车运回.经了解,当地运输公司有大、小两种型号货车,其运力和租金如表:
(1)、过点C作 , 垂足为E;(尺规作图,保留作图痕迹,不写作法)(2)、当时,求的长.23. 某水果商从外地购进某种水果若干箱,需要租赁货车运回.经了解,当地运输公司有大、小两种型号货车,其运力和租金如表:运力(箱辆)
租金(元辆)
大货车
45
400
小货车
35
320
(1)、若该水果商计划租用大、小货车共8辆,其中大货车辆,共需付租金元,请写出与的函数关系式;(2)、在(1)的条件下,若这批水果共340箱,所租用的8辆货车可一次将购进的水果全部运回,请给出最节省费用的租车方案,并求出最低费用.24. 已知菱形ABCD,∠BAD=60°,直线BH不经过点A,D,点A关于直线BH的对称点为E,CE交直线BH于点P,连接AP. (1)、如图1,当直线BH经过点C时,点E恰好在DB的延长线上,点P与点C重合,则∠AEP= ▲ °,线段EA与EP之间的数量关系为 ▲ , 说明理由;(2)、当直线BH不经过点C,且在菱形ABCD外部,时,如图2,
(1)、如图1,当直线BH经过点C时,点E恰好在DB的延长线上,点P与点C重合,则∠AEP= ▲ °,线段EA与EP之间的数量关系为 ▲ , 说明理由;(2)、当直线BH不经过点C,且在菱形ABCD外部,时,如图2,①依题意补全图2;
②(1)中的结论是否发生改变?若不改变,请证明;若改变,说明理由.
25. 如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,点 , . (1)、求直线AC的表达式;(2)、点M从点O出发以每秒1个单位长度的速度沿x轴向右运动,点N从点A出发以每秒3个单位长度的速度沿x轴向左运动,两点同时出发.过点M,N作x轴的垂线分别交直线OC,AC于点P,Q,猜想四边形PMNQ的形状(点M,N重合时除外),并证明你的猜想;(3)、在(2)的条件下,当点M运动多少秒时,四边形PMNQ是正方形.
(1)、求直线AC的表达式;(2)、点M从点O出发以每秒1个单位长度的速度沿x轴向右运动,点N从点A出发以每秒3个单位长度的速度沿x轴向左运动,两点同时出发.过点M,N作x轴的垂线分别交直线OC,AC于点P,Q,猜想四边形PMNQ的形状(点M,N重合时除外),并证明你的猜想;(3)、在(2)的条件下,当点M运动多少秒时,四边形PMNQ是正方形.