江苏省南京市秦淮区2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-06-28 类型:期末考试
一、单选题
-
1. 北京 2022年冬奥会会徽是以汉字“冬”为灵感来源设计的.在下面的四个图中,由下图经过平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 据了解,新型冠状病毒(SARS﹣CoV﹣2)的最大直径大约是0.00000014米.数0.00000014用科学记数法表示为( )A、1.4×10 B、1.4×10 C、1.4×10 D、14×103. 如图,平行线AB , CD被直线AE所截,∠1=80°,则∠2的度数是( )
2. 据了解,新型冠状病毒(SARS﹣CoV﹣2)的最大直径大约是0.00000014米.数0.00000014用科学记数法表示为( )A、1.4×10 B、1.4×10 C、1.4×10 D、14×103. 如图,平行线AB , CD被直线AE所截,∠1=80°,则∠2的度数是( )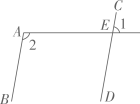 A、80° B、90° C、100° D、110°4. 若 是方程3x+ay=5的解,则a的值是( )A、1 B、﹣1 C、4 D、﹣45. 已知 , 则下列不等式成立的是( )A、 B、 C、 D、6. 已知 , 那么a,b,c之间的大小关系是( )A、 B、 C、 D、7. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=2 B、a=-3,b=2 C、a=3,b=-1 D、a=-1,b=38. 一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合. 则下列判断正确的是( )
A、80° B、90° C、100° D、110°4. 若 是方程3x+ay=5的解,则a的值是( )A、1 B、﹣1 C、4 D、﹣45. 已知 , 则下列不等式成立的是( )A、 B、 C、 D、6. 已知 , 那么a,b,c之间的大小关系是( )A、 B、 C、 D、7. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=2 B、a=-3,b=2 C、a=3,b=-1 D、a=-1,b=38. 一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合. 则下列判断正确的是( ) A、纸带①的边线平行,纸带②的边线不平行 B、纸带①、②的边线都平行 C、纸带①的边线不平行,纸带②的边线平行 D、纸带①、②的边线都不平行
A、纸带①的边线平行,纸带②的边线不平行 B、纸带①、②的边线都平行 C、纸带①的边线不平行,纸带②的边线平行 D、纸带①、②的边线都不平行二、填空题
-
9. 计算的结果是.10. 分解因式的结果是.11. 如图,点D在 的延长线上, 于点E,交 于点F,若 , ,则 的度数为 .
 12. 一个多边形的内角和与外角和之和为900°,则这个多边形的边数为.13. 若 , 则.14. 已知a+b=4,若﹣2≤b≤﹣1,则a的取值范围是.15. 如图,6块同样大小的长方形复合地板刚好拼成一个宽为 的大长方形,则这个大长方形的长是 .
12. 一个多边形的内角和与外角和之和为900°,则这个多边形的边数为.13. 若 , 则.14. 已知a+b=4,若﹣2≤b≤﹣1,则a的取值范围是.15. 如图,6块同样大小的长方形复合地板刚好拼成一个宽为 的大长方形,则这个大长方形的长是 .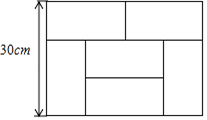 16. 如图,在中,E是上的一点, , D是的中点,且 , 则.
16. 如图,在中,E是上的一点, , D是的中点,且 , 则. 17. 对于实数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[5]=5,[-π]=-4.如果[a]=-2,那么a的取值范围是 .18. 如图,在中, , M是射线上的一个动点,过点M作交射线于点N,连接 , 若中有两个角相等,则的度数可能是.
17. 对于实数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[5]=5,[-π]=-4.如果[a]=-2,那么a的取值范围是 .18. 如图,在中, , M是射线上的一个动点,过点M作交射线于点N,连接 , 若中有两个角相等,则的度数可能是.
三、解答题
-
19. 计算:(1)、;(2)、.20. 解方程组21. 先化简,再求值: , 其中.22. 解不等式组并写出它的整数解.23. 如图,已知 , , 求证:.

证明:∵(已知),
又∵ ▲ ( ),
∴(等量代换).
∴( ).
∴( ).
又∵(已知),
∴ ▲ (等量代换).
∴( ).
24. 如图,在中,是高,、是角平分线,它们相交于点 , , . (1)、求的度数;(2)、求的度数.25. 问题提出
(1)、求的度数;(2)、求的度数.25. 问题提出在学完乘法公式后,王老师向同学们提出了这样一个问题:你能求代数式的最大值吗?
初步思考
同学们经过交流、讨论,总结出如下方法:
解:
因为 ,
所以.
所以当时,的值最大,最大值是0.
所以当时,的值最大,最大值是4.
所以的最大值是4.
(1)、尝试应用
求代数式的最大值,并写出相应的x的值.(2)、拓展提高
将一根长的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,那么这两个正方形面积之和有最小值吗?若有,求此时这根铁丝剪成两段后的长度及这两个正方形面积的和;若没有,请说明理由.26. 截至12月25日,全国累计报告接种新型冠状病毒疫苗超过12亿剂次.为了满足市场需求,某公司计划投入10个大、小两种车间共同生产同一种新型冠状病毒疫苗,已知1个大车间和2个小车间每周能生产疫苗共35万剂,2个大车间和1个小车间每周能生产疫苗共40万剂,每个大车间生产1万剂疫苗的平均成本为90万元,每个小车间生产1万剂疫苗的平均成本为80万元.(1)、该公司每个大车间、小车间每周分别能生产疫苗多少万剂?(2)、若投入的10个车间每周生产的疫苗不少于135万剂,请问一共有几种投入方案,并求出每周生产疫苗的总成本最小值?27. 如图1,已知两条直线 , 被直线所截,分别交于点 , 点 , 平分交于点 , 且 .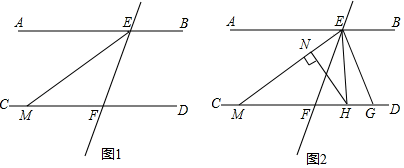 (1)、判断直线与直线是否平行,并说明理由;(2)、如图2,点是射线上一动点(不与点 , 重合),平分交于点 , 过点作于点 , 设 , .
(1)、判断直线与直线是否平行,并说明理由;(2)、如图2,点是射线上一动点(不与点 , 重合),平分交于点 , 过点作于点 , 设 , .①当点在点的右侧时,若 , 求的度数;
②当点在运动过程中,和之间有怎样的数量关系?请写出你的猜想,并加以证明.