河南省信阳市新县2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-06-28 类型:期末考试
一、单选题
-
1. 下列事件中适合采用抽样调查的是( )A、对乘坐飞机的乘客进行安检 B、学校招聘教师,对应聘人员进行面试 C、对“天宫2号”零部件的检查 D、对端午节期间市面上粽子质量情况的调查2. 下列各数: , 1.212212221…, , π,中,有理数的个数为( )A、1个 B、2个 C、3个 D、4个3. 如图,下列条件中能判断AB∥CD的是( )
 A、∠BAD+∠ABC=180° B、∠BAC=∠ACD C、∠1=∠2 D、∠3=∠44. 不等式组 的解在数轴上表示为( )A、
A、∠BAD+∠ABC=180° B、∠BAC=∠ACD C、∠1=∠2 D、∠3=∠44. 不等式组 的解在数轴上表示为( )A、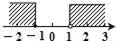 B、
B、 C、
C、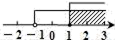 D、
D、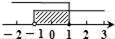 5. 若点P在第二象限,且点P到x轴、y轴的距离分别为4,3,则点P的坐标是( )A、(4,3) B、(3,﹣4) C、(﹣3,4) D、(﹣4,3)6. 将一张面值100元的人民币,兑换成10元或20元的零钱,兑换方案有( )A、4种 B、5种 C、6种 D、7种7. 若方程6kx﹣2y=8有一组解 ,则k的值等于(( )A、 B、 C、 D、8. 小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图1;小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图2那样的正方形,中间还留下了一个洞,恰好是边长为3mm的小正方形,则每个小长方形的面积为( )
5. 若点P在第二象限,且点P到x轴、y轴的距离分别为4,3,则点P的坐标是( )A、(4,3) B、(3,﹣4) C、(﹣3,4) D、(﹣4,3)6. 将一张面值100元的人民币,兑换成10元或20元的零钱,兑换方案有( )A、4种 B、5种 C、6种 D、7种7. 若方程6kx﹣2y=8有一组解 ,则k的值等于(( )A、 B、 C、 D、8. 小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图1;小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图2那样的正方形,中间还留下了一个洞,恰好是边长为3mm的小正方形,则每个小长方形的面积为( ) A、 B、 C、 D、9. 数轴上点A表示的数为- , 点B表示的数为 , 则A、B之间表示整数的点有( )A、21个 B、20个 C、19个 D、18个10. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点 出发,按向右,向上,向右,向下的方向依次不断移动,每次移动 .其行走路线如图所示,第1次移动到 ,第2次移动到 ,…,第 次移动到 .则 的面积是( )
A、 B、 C、 D、9. 数轴上点A表示的数为- , 点B表示的数为 , 则A、B之间表示整数的点有( )A、21个 B、20个 C、19个 D、18个10. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点 出发,按向右,向上,向右,向下的方向依次不断移动,每次移动 .其行走路线如图所示,第1次移动到 ,第2次移动到 ,…,第 次移动到 .则 的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 的平方根是 .12. 一组数据共50个,分别落在5个小组内,第一、二、三、五组的频数分别为2,8,15,5,则第四小组的频数以及所占的百分比分别为.13. 将一张长方形纸片折叠成如图所示的形状,若 , 则.
 14. 关于x、y的方程组 的解x与y满足条件x+y≤5,则3m﹣4的最大值是.15. 小明将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起,当∠ACE<180°且点E在直线AC的上方时,他发现若∠ACE= , 则三角板BCE有一条边与斜边AD平行.
14. 关于x、y的方程组 的解x与y满足条件x+y≤5,则3m﹣4的最大值是.15. 小明将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起,当∠ACE<180°且点E在直线AC的上方时,他发现若∠ACE= , 则三角板BCE有一条边与斜边AD平行.
三、解答题
-
16. 计算:(1)、;(2)、4(x+1)2﹣64=0.17.(1)、解方程组:;(2)、求不等式组的解集,并求出它的所有整数解.18. 如图,在平面直角坐标系中,已知点的坐标为.
 (1)、三角形是由三角形向下平移3个单位长度,再向左平移1个单位长度后得到的,请画出三角形 , 并写出 , , 的坐标;(2)、求三角形的面积;(3)、若点在坐标轴的正半轴上,且三角形的面积为2,直接写出符合条件的点的坐标.19. 已知,如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
(1)、三角形是由三角形向下平移3个单位长度,再向左平移1个单位长度后得到的,请画出三角形 , 并写出 , , 的坐标;(2)、求三角形的面积;(3)、若点在坐标轴的正半轴上,且三角形的面积为2,直接写出符合条件的点的坐标.19. 已知,如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D. (1)、求证:AC//DF.(2)、若∠DEC=150°,求∠GBA.20. 已知的算术平方根是3,b是8的立方根,c是的整数部分.(1)、求的值.(2)、求的平方根.21. 市教育局想知道某校学生对“中原第一高楼﹣﹣玉米楼”的了解程度,在该校随机抽取了部分学生进行问卷,问卷有以下四个选项:A.十分了解;B.了解较多;C.了解较少;D.不了解(要求:每名被调查的学生必选且只能选择一项).现将调查的结果绘制成两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题:
(1)、求证:AC//DF.(2)、若∠DEC=150°,求∠GBA.20. 已知的算术平方根是3,b是8的立方根,c是的整数部分.(1)、求的值.(2)、求的平方根.21. 市教育局想知道某校学生对“中原第一高楼﹣﹣玉米楼”的了解程度,在该校随机抽取了部分学生进行问卷,问卷有以下四个选项:A.十分了解;B.了解较多;C.了解较少;D.不了解(要求:每名被调查的学生必选且只能选择一项).现将调查的结果绘制成两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题: (1)、本次被抽取的学生共有名;m=;(2)、请补全条形图;(3)、扇形图中的选项“C.了解较少”部分所占扇形的圆心角的大小是多少?(4)、若该校共有2000名学生,请你根据上述调查结果估计该校对于“中原第一高楼”“十分了解”和“了解较多”的学生共有多少名?22. 今年春节期间,我国武汉地区因“新冠疫情”全面封城,牵动了无数中华儿女的心,全国各地各行各业发起了献爱心捐赠活动.某果农为武汉捐赠了一批水果和蔬菜共320箱,其中水果比蔬菜多80箱.(1)、求水果和蔬菜各有多少箱?(2)、现计划租用甲、乙两种货车共8辆,一次性将这批物资全部运往武汉.已知每辆甲种货车可满载40箱水果和10箱蔬菜,每辆乙种货车可满载水果和蔬菜各20箱,则运输部门安排甲、乙两种货车时有哪几种方案?请你设计出来.(3)、在(2)的条件下,如果甲种货车每辆需付运费1200元,乙种货车每辆需付运费1000元,选择哪种运输方案运费最少?最少运费是多少?(通过计算具体数据说明结论)23. 在平面直角坐标系中,D(0,﹣3),M(4,﹣3),直角三角形ABC的边与x轴分别相交于O、G两点,与直线DM分别交于E、F点,∠ACB=90°.
(1)、本次被抽取的学生共有名;m=;(2)、请补全条形图;(3)、扇形图中的选项“C.了解较少”部分所占扇形的圆心角的大小是多少?(4)、若该校共有2000名学生,请你根据上述调查结果估计该校对于“中原第一高楼”“十分了解”和“了解较多”的学生共有多少名?22. 今年春节期间,我国武汉地区因“新冠疫情”全面封城,牵动了无数中华儿女的心,全国各地各行各业发起了献爱心捐赠活动.某果农为武汉捐赠了一批水果和蔬菜共320箱,其中水果比蔬菜多80箱.(1)、求水果和蔬菜各有多少箱?(2)、现计划租用甲、乙两种货车共8辆,一次性将这批物资全部运往武汉.已知每辆甲种货车可满载40箱水果和10箱蔬菜,每辆乙种货车可满载水果和蔬菜各20箱,则运输部门安排甲、乙两种货车时有哪几种方案?请你设计出来.(3)、在(2)的条件下,如果甲种货车每辆需付运费1200元,乙种货车每辆需付运费1000元,选择哪种运输方案运费最少?最少运费是多少?(通过计算具体数据说明结论)23. 在平面直角坐标系中,D(0,﹣3),M(4,﹣3),直角三角形ABC的边与x轴分别相交于O、G两点,与直线DM分别交于E、F点,∠ACB=90°. (1)、将直角三角形如图1位置摆放,如果∠AOG=46°,则∠CEF=;(2)、将直角三角形ABC如图2位置摆放,N为AC上一点,∠NED+∠CEF=180°,请写出∠NEF与∠AOG之间的等量关系,并说明理由.(3)、将直角三角形ABC如图3位置摆放,若∠GOC=140°,延长AC交DM于点Q,点P是射线GF上一动点,探究∠POQ,∠OPQ与∠PQF的数量关系,请直接写出结论(题中的所有角都大于0°小于180°).
(1)、将直角三角形如图1位置摆放,如果∠AOG=46°,则∠CEF=;(2)、将直角三角形ABC如图2位置摆放,N为AC上一点,∠NED+∠CEF=180°,请写出∠NEF与∠AOG之间的等量关系,并说明理由.(3)、将直角三角形ABC如图3位置摆放,若∠GOC=140°,延长AC交DM于点Q,点P是射线GF上一动点,探究∠POQ,∠OPQ与∠PQF的数量关系,请直接写出结论(题中的所有角都大于0°小于180°).