河南省新乡市卫辉市2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-06-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 关于x的方程 $n x^{n} - 1 + n - 4 = 0$ 是一元一次方程，则这个方程的解是（）

A、 $x = - 1$ B、 $x = 1$ C、 $x = - 4$ D、 $x = 4$

查看试题解析
3. 若一个正多边形的每个内角为150°，则这个正多边形的边数是（）

A、12 B、11 C、10 D、9

查看试题解析
4. 如图，在 $△ A B C$ 中， $∠ A = 60 °$ ，则图中 $∠ 1 + ∠ 2$ 的度数是（）

A、180° B、240° C、220° D、300°

查看试题解析
5. 将 $R t △ A B C$ 沿 $C B$ 方向平移后得到 $R t △ D E F$ ，已知 $A M = 3$ ， $B E = 6$ ， $D E = 10$ .则图中阴影部分的面积为（）

A、39 B、51 C、45 D、42

查看试题解析
6. 如图，10块形状、大小相同的小长方形墙砖拼成一个大长方形，设小长方形墙砖的长和宽分别为x厘米和y厘米，则依题意可列方程组为（）

A、 ${\begin{array}{l} x + 2 y = 75 \\ y = 3 x \end{array}$ B、 ${\begin{array}{l} x + 2 y = 75 \\ x = 3 y \end{array}$ C、 ${\begin{array}{l} 2 x - y = 75 \\ y = 3 x \end{array}$ D、 ${\begin{array}{l} 2 x + y = 75 \\ x = 3 y \end{array}$

查看试题解析
7. 关于x、y的二元一次方程组 ${\begin{array}{l} x + a y = 0 \\ x + y = 3 \end{array}$ 的解是 ${\begin{array}{l} x = 1 \\ y = ● \end{array}$ ，其中y的值被墨水盖住了，请同学们求出a的值为（）

A、-2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
8. 关于x、y的二元一次方程组 ${\begin{array}{l} y - 2 x = m ， \\ 2 y + 3 x = m + 1 ， \end{array}$ 满足 $x + 3 y \geq 0$ ，则m的取值范围为（）

A、 $m \geq \frac{1}{2}$ B、 $m \geq 1$ C、 $- \frac{1}{2} ≤ m ≤ 1$ D、 $m \geq - \frac{1}{2}$

查看试题解析
9. 在 $△ A B C$ 中， $A C = 6$ ， $B C = 4$ ，将 $△ A B C$ 折叠，使点A落在点B处，折痕为 $D F$ ，连结 $B F$ ，则 $△ B C F$ 的周长为（）

A、20 B、16 C、10 D、8

查看试题解析
10. 若关于x的一元一次不等式组 ${\begin{matrix} x - 2 k \leq 0 \\ x + k > 2 \end{matrix}$ 有解，则k的取值范围为（）

A、 $k > - \frac{2}{3}$ B、 $k > \frac{2}{3}$ C、 $k \leq \frac{2}{3}$ D、 $k \geq - \frac{2}{3}$

查看试题解析

二、填空题

11. 请用不等式表示“x的2倍与3的差不大于8”为.

查看试题解析
12. 已知 $△ A B C ≅ △ D E F$ ， $A B = 5$ ， $B C = 6$ ， $D F = 4$ ，则 $E F =$ .

查看试题解析
13. 等腰三角形的周长为 $19 c m$ ，若有一边长为 $9 c m$ ，则等腰三角形的其他两边长分别是.

查看试题解析
14. 一个多边形的外角和是内角和的 $\frac{2}{7}$ ，则这个多边形的边数为．

查看试题解析
15. 关于x的一元一次方程 $\frac{x}{2022} - 1 = 2022 x + m$ 的解为 $x = - 2019$ ，则关于y的方程 $\frac{3 - y}{2022} - 1 = 2022 (3 - y) + m$ 的解为.

查看试题解析

三、解答题

16. 解方程和不等式组

(1)、解方程 $\frac{2 x + 5}{6} - \frac{3 x - 2}{8} = 2$

(2)、解不等式组 ${\begin{array}{l} 3 (x + 1) < 5 x + 4 ① \\ \frac{x - 1}{2} \geq \frac{2 x - 1}{5} ② \end{array}$ 并把不等式组的解集在数轴上表示出来.

查看试题解析
17. 课堂上老师写一道题目：解方程组 ${\begin{array}{l} x + y = 15 ① \\ 16 x + 6 y = 140 ② \end{array}$

(1)、小组合作时，发现有同学这么做：
$① \times 6$ 得， $6 x + 6 y = 90$ ③
$② - ③$ 得， $10 x = 50$
$x = 5$
把 $x = 5$ 代入①得 $y = 10$
∴这个方程组的解是 ${\begin{array}{l} x = 5 \\ y = 10 \end{array}$
该同学解这个方程组的过程中使用了消元法，目的是把二元一次方程组转化为.

(2)、请用另一种方法解这个方程组.

查看试题解析
18. 如图，在△ABC中，∠B＝24°，∠ACB＝104°，AD⊥BC交BC的延长线于点D，AE平分∠BAC.

(1)、求∠DAE的度数.

(2)、若∠B＝α，∠ACB＝β，其它条件不变，请直接写出∠DAE与α、β的数量关系.

查看试题解析
19. 如图，所示的正方形网格中，每个小正方形的边长均为1个单位，△ABC的三个顶点都在格点上，请按要求画图：

(1)、在网格中画出△ABC向下平移5个单位得到的 $△ A_{1} B_{1} C_{1}$ ；

(2)、在网格中画出 $△ A_{1} B_{1} C_{1}$ 关于直线l对称的 $△ A_{2} B_{2} C_{2}$ ；

(3)、在网格中画出将△ABC绕点A按逆时针方向旋转90°得到的 $△ A B_{3} C_{3}$ ．

查看试题解析
20. 如图，四边形 $A B C D$ 是正方形，E、F分别是边 $B C$ ， $C D$ 上的点， $∠ 1 = ∠ 2$ ，将 $△ A D F$ 沿顺时针方向旋转90°，得到 $△ A B P$ .

(1)、请说明 $∠ B A E + ∠ 1$ 与 $∠ A F D$ 的大小关系；

(2)、 $B E + D F$ 与 $A E$ 相等吗？请说明理由.

查看试题解析
21. 定义：如果两个一元一次方程的解互为相反数，我们称这两个方程为“兄弟方程”，如方程 $x = 2$ 和 $4 x + 8 = 0$ 为“兄弟方程”.

(1)、关于x的方程 $3 x + m = 0$ 与方程 $\frac{1}{2} x - 1 = 1 - \frac{3}{2} x$ 是“兄弟方程”.求m的值；

(2)、若两个“兄弟方程”的两个解的差为6，其中一个解为a，求a的值；

(3)、关于x的方程 $2 x + 3 m - 2 = 0$ 和 $3 x - 5 m + 4 = 0$ 是“兄弟方程”，求这两个方程的解.

查看试题解析
22. 为了加强对校内外的安全监控，创建“平安校园”，某学校计划增加15台监控摄像设备，现有甲、乙两种型号的设备，其中每台价格、有效监控半径如表格所示.经调查，购买1台甲型设备比购买1台乙型设备少150元，购买3台甲型设备比购买2台乙型设备多150元.

甲型
乙型
价格（单位：元/台）
a
b
有效监控半径（单位：米/台）
100
150

(1)、求a，b的值；

(2)、若购买该批设备的资金不超过7200元，则至少购买甲型设备多少台？

(3)、在（2）购买设备资金不超过7200元的条件下，若要求有效监控半径覆盖范围不低于1600米，为了节约资金，请你设计一种最省钱的购买方案.

查看试题解析
23. 如图1，将两个直角三角板放在同一直线 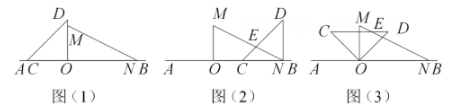$A B$ 上；其中 $∠ O N M = 30 °$ ， $∠ O C D = 45 °$ .

(1)、观察猜想：将图1中的三角板 $O C D$ 沿直线 $A B$ 向右平移至图2的位置，使得点O与点N重合， $C D$ 与 $M N$ 相交于点E，则 $∠ C E N =$

(2)、操作探究：将图1中的三角板 $O C D$ 绕点O按顺时针方向旋转，使一边 $O D$ 在 $∠ M O N$ 的内部，如图3，且 $O D$ 恰好平分 $∠ M O N$ ， $C D$ 与 $M N$ 相交于点E，求 $∠ C E N$ 的度数；

(3)、深化拓展：将图1中的三角板 $O C D$ 绕点O按顺时针方向旋转一周，在旋转的过程中，当边 $O C$ 旋转角度为时，边 $C D$ 恰好与边 $M N$ 平行.（直接写出结果）

查看试题解析

	甲型	乙型
价格（单位：元/台）	a	b
有效监控半径（单位：米/台）	100	150