天津市河西区2022届高三下学期数学二模试卷
试卷更新日期:2022-06-27 类型:高考模拟
一、单选题
-
1. 设集合 , , 则( )A、{2} B、 C、 D、2. 已知 且 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件3. 函数在上的大致图象为( )A、
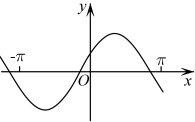 B、
B、 C、
C、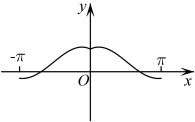 D、
D、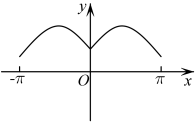 4. 某高中学校学生人数和近视情况分别如图①和图②所示.为了解该学校学生近视形成原因,在近视的学生中按年级用分层抽样的方法抽取部分学生进行问卷调查,已知抽取到的高中一年级的学生36人,则抽取到的高三学生数为( )
4. 某高中学校学生人数和近视情况分别如图①和图②所示.为了解该学校学生近视形成原因,在近视的学生中按年级用分层抽样的方法抽取部分学生进行问卷调查,已知抽取到的高中一年级的学生36人,则抽取到的高三学生数为( ) A、32 B、45 C、64 D、905. 已知 , , , 则( )A、 B、 C、 D、6. 对于函数 , 有下列结论:①最小正周期为;②最大值为2;③减区间为;④对称中心为 . 则上述结论正确的个数是( )A、1 B、2 C、3 D、47. 如图,已知某圆锥形容器的轴截面是面积为的正三角形,在该容器内放置一个圆柱,使得圆柱的上底面与圆锥的底面重合,且圆柱的高是圆锥的高的 , 则圆柱的体积为( )
A、32 B、45 C、64 D、905. 已知 , , , 则( )A、 B、 C、 D、6. 对于函数 , 有下列结论:①最小正周期为;②最大值为2;③减区间为;④对称中心为 . 则上述结论正确的个数是( )A、1 B、2 C、3 D、47. 如图,已知某圆锥形容器的轴截面是面积为的正三角形,在该容器内放置一个圆柱,使得圆柱的上底面与圆锥的底面重合,且圆柱的高是圆锥的高的 , 则圆柱的体积为( )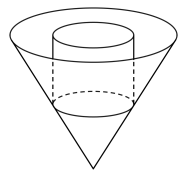 A、4π B、8π C、 D、8. 已知抛物线上一点到焦点的距离为3,准线为l,若l与双曲线的两条渐近线所围成的三角形面积为 , 则双曲线C的离心率为( )A、3 B、 C、 D、9. 已知定义在R上的函数满足:①;②;③在上的解析式为 , 则函数与函数的图象在区间上的交点个数为( )A、3 B、4 C、5 D、6
A、4π B、8π C、 D、8. 已知抛物线上一点到焦点的距离为3,准线为l,若l与双曲线的两条渐近线所围成的三角形面积为 , 则双曲线C的离心率为( )A、3 B、 C、 D、9. 已知定义在R上的函数满足:①;②;③在上的解析式为 , 则函数与函数的图象在区间上的交点个数为( )A、3 B、4 C、5 D、6二、填空题
-
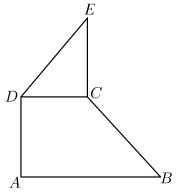
10. 是虚数单位,复数 .11. 若 , 则 .12. 设与相交于两点,则 .13. 若函数在处取得极值,则 .14. 已知一箱产品中含有2件次品和3件正品,现需要通过检测将其区分.每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束,则第一次检测出的是次品且第二次检测出正品的概率是;已知每检测一件产品需花费100元,设表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),则 .15. 如图直角梯形中, , , , 在等腰直角三角形中, , 则向量在向量上的投影向量的模为;若 , 分别为线段 , 上的动点,且 , 则的最小值为 .
三、解答题
-
16. 在 中,内角 所对的边分别为 .已知 , .
(I)求 的值;
(II)求 的值.
17. 如图所示,在几何体ABCDEF中,四边形ABCD为直角梯形,AD∥BC,AB⊥AD,AE⊥底面ABCD,AE∥CF,AD=3,AB=BC=AE=2,CF=1. (1)、求证:BF∥平面ADE;(2)、求直线BE与直线DF所成角的余弦值;(3)、求点D到直线BF的距离.18. 已知椭圆:的左、右焦点分别为、 , 是椭圆上一点,且与轴垂直.(1)、求椭圆的标准方程;(2)、设椭圆的右顶点为A,为坐标原点,过作斜率大于0直线交椭圆于、两点,直线与坐标轴不重合,若与的面积比为 , 求直线的方程.
(1)、求证:BF∥平面ADE;(2)、求直线BE与直线DF所成角的余弦值;(3)、求点D到直线BF的距离.18. 已知椭圆:的左、右焦点分别为、 , 是椭圆上一点,且与轴垂直.(1)、求椭圆的标准方程;(2)、设椭圆的右顶点为A,为坐标原点,过作斜率大于0直线交椭圆于、两点,直线与坐标轴不重合,若与的面积比为 , 求直线的方程.