天津市河东区2022届高三下学期数学二模试卷
试卷更新日期:2022-06-27 类型:高考模拟
一、单选题
-
1. 设集合 , , , 则( )A、 B、 C、 D、2. 已知命题 , 命题 , 则命题p是命题q成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 函数 在 的图象大致为( )A、
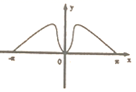 B、
B、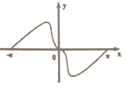 C、
C、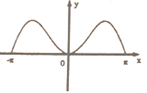 D、
D、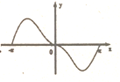 4. 为了解一片经济树林的生长情况,随机测量了其中100株树木的底部周长(单位:cm),根据所得数据画出样本的频率分布直方图如图所示.那么在这100株树木中,底部周长小于110cm的株数n是( )
4. 为了解一片经济树林的生长情况,随机测量了其中100株树木的底部周长(单位:cm),根据所得数据画出样本的频率分布直方图如图所示.那么在这100株树木中,底部周长小于110cm的株数n是( )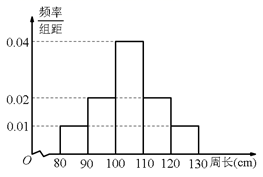 A、30 B、60 C、70 D、805. 设 , , , 则a,b,c大小关系为( )A、 B、 C、 D、6. 攒尖是我国古代建筑中屋顶的一种结构样式,多见于亭阁式建筑、园林建筑.下面以圆形攒尖为例.如图所示的建筑屋顶可近似看作一个圆锥,其轴截面(过圆锥旋转轴的截面)是底边长为 , 顶角为的等腰三角形,则该屋顶的体积约为( )
A、30 B、60 C、70 D、805. 设 , , , 则a,b,c大小关系为( )A、 B、 C、 D、6. 攒尖是我国古代建筑中屋顶的一种结构样式,多见于亭阁式建筑、园林建筑.下面以圆形攒尖为例.如图所示的建筑屋顶可近似看作一个圆锥,其轴截面(过圆锥旋转轴的截面)是底边长为 , 顶角为的等腰三角形,则该屋顶的体积约为( ) A、 B、 C、 D、7. 已知离心率为的双曲线的左、右焦点分别是 , 若点是抛物线的准线与的渐近线的一个交点,且满足 , 则双曲线的方程是A、 B、 C、 D、8. 已知函数的最小正周期为 , 且它的图象关于直线对称,则下列说法正确的个数为( )
A、 B、 C、 D、7. 已知离心率为的双曲线的左、右焦点分别是 , 若点是抛物线的准线与的渐近线的一个交点,且满足 , 则双曲线的方程是A、 B、 C、 D、8. 已知函数的最小正周期为 , 且它的图象关于直线对称,则下列说法正确的个数为( )①将的图象向右平移个单位长度后,得到函数的图象; ②的图象经过点;③的图象的一个对称中心是;④在上是减函数;
A、1 B、2 C、3 D、49. 已知函数 , 若方程有4个实根,则的取值范围是A、 B、 C、 D、二、填空题
-
10. i是虚数单位,则复数 .11. 在的二项展开式中,含的项的系数是 . (用数字作答)12. 圆与圆的公共弦长为 .13. 设正实数满足 , 则的最小值为 .14. 甲、乙、丙三人投篮的命中率分别为 , , , 现要求三人各投篮一次.假设每人投篮相互独立,则至少有一人命中的概率为;记三人命中总次数为 , 则.15. 在中,点M,N是线段上的两点, , , 则 , 的取值范围是.
三、解答题
-
16. 在中,角的对边分别为 , , , 的面积为 .(1)、求及的值;(2)、求的值.17. 如图所示,直角梯形ABCD中, , AD垂直AB, , 四边形EDCF为矩形, , 平面平面ABCD.
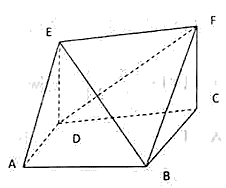 (1)、求证:∥平面ABE;(2)、求平面ABE与平面EFB所成二面角的正弦值;(3)、在线段DF上是否存在点P,使得直线BP与平面ABE所成角的正弦值为 , 若存在,求出线段BP的长,若不存在,请说明理由.
(1)、求证:∥平面ABE;(2)、求平面ABE与平面EFB所成二面角的正弦值;(3)、在线段DF上是否存在点P,使得直线BP与平面ABE所成角的正弦值为 , 若存在,求出线段BP的长,若不存在,请说明理由.