天津市和平区2022届高三下学期数学三模试卷
试卷更新日期:2022-06-27 类型:高考模拟
一、单选题
-
1. 已知全集 , 集合 , 则( )A、{5} B、 C、 D、2. 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件3. 函数的图象大致为( )A、
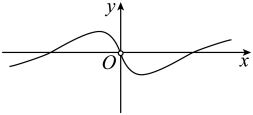
B、
B、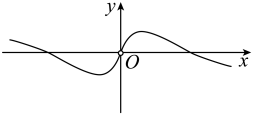
C、
C、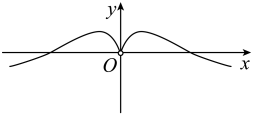
D、
D、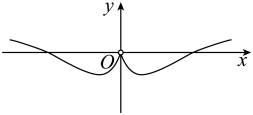
4. 某校高一年级学生打算利用周六休息时间做义工,为了了解高一年级学生做义工时长的情况,随机抽取了高一年级100名学生进行调查,将收集到的做义工时间(单位:小时)数据分成6组: , , , , , , (时间均在内),如图,已知上述时间数据的第70百分位数为3.5,则 , 的值分别为( )
4. 某校高一年级学生打算利用周六休息时间做义工,为了了解高一年级学生做义工时长的情况,随机抽取了高一年级100名学生进行调查,将收集到的做义工时间(单位:小时)数据分成6组: , , , , , , (时间均在内),如图,已知上述时间数据的第70百分位数为3.5,则 , 的值分别为( ) A、0.3,0.35 B、0.4,0.25 C、0.35,0.3 D、0.35,0.255. 设 , 则的大小关系为( )A、 B、 C、 D、6. 已知某圆柱的轴截面为正方形,则此圆柱的表面积与此圆柱外接球的表面积之比为( )A、3:4 B、1:2 C、 D、2:17. 已知双曲线与抛物线有一个公共的焦点 , 且两曲线的一个交点为.若 , 则双曲线的渐近线方程为( )A、 B、 C、 D、8. 函数 , 将函数的图象向左平移个单位长度,得到函数的图象,若为偶函数,则的最小值是( )A、 B、 C、 D、9. 已知函数 , 关于的方程R)有四个相异的实数根,则的取值范围是( )A、 B、 C、 D、
A、0.3,0.35 B、0.4,0.25 C、0.35,0.3 D、0.35,0.255. 设 , 则的大小关系为( )A、 B、 C、 D、6. 已知某圆柱的轴截面为正方形,则此圆柱的表面积与此圆柱外接球的表面积之比为( )A、3:4 B、1:2 C、 D、2:17. 已知双曲线与抛物线有一个公共的焦点 , 且两曲线的一个交点为.若 , 则双曲线的渐近线方程为( )A、 B、 C、 D、8. 函数 , 将函数的图象向左平移个单位长度,得到函数的图象,若为偶函数,则的最小值是( )A、 B、 C、 D、9. 已知函数 , 关于的方程R)有四个相异的实数根,则的取值范围是( )A、 B、 C、 D、二、填空题
-
10. 已知为虚数单位,设复数满足 , 则的虚部为 .11. 的展开式中项的系数为 .12. 已知圆 的圆心坐标是 ,若直线 与圆 相切于点 ,则圆C的标准方程为.13. 设 ,则 的最大值为 .14. 清明节前夕,某校团委决定举办“缅怀革命先烈,致敬时代英雄”主题演讲比赛,经过初赛,共7人进入决赛,其中高一年级2人,高二年级3人,高三年级2人,现采取抽签方式决定演讲顺序,设事件为“高二年级3人相邻”,事件的排法为种;在事件“高二年级3人相邻”的前提下,事件“高一年级2人不相邻”的概率为 .15. 在平面内,定点 , 满足 , 且 , 则;平面内的动点满足 , , 则的最大值是 .
三、解答题
-
16. 在中, , , .(1)、求AB的长;(2)、求;(3)、求的值.17. 如图,正四棱柱中,且 , 点分别是的中点.
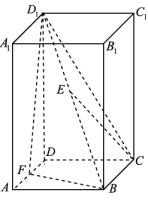 (1)、求直线与直线所成角的正切值;(2)、求平面与平面的夹角的余弦值;(3)、求点到平面的距离.18. 已知椭圆的离心率为 , 且椭圆过点 .(1)、求椭圆的标准方程;(2)、过右焦点的直线与椭圆交于两点,线段的垂直平分线交直线于点 , 交直线于点 , 求的最小值.
(1)、求直线与直线所成角的正切值;(2)、求平面与平面的夹角的余弦值;(3)、求点到平面的距离.18. 已知椭圆的离心率为 , 且椭圆过点 .(1)、求椭圆的标准方程;(2)、过右焦点的直线与椭圆交于两点,线段的垂直平分线交直线于点 , 交直线于点 , 求的最小值.