天津市部分区2022届高三下学期数学高考前质检试卷
试卷更新日期:2022-06-27 类型:高考模拟
一、单选题
-
1. 已知集合 , , 则=( )A、或 B、或 C、 D、或2. 下列函数中,既是偶函数又在 , 上单调递增的函数是( )A、 B、 C、 D、3. 命题的否定是( )A、 B、 C、 D、4. 正项等比数列 , 若 , 则“公比”是“的最小值为2”的( )A、充分不必要条件 B、必要不充分条 C、充要条件 D、既不充分也不必要条件5. 为征求个人所得税法修改建议,某机构调查了10000名当地职工的月收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:①估计样本的中位数为4800元;②如果个税起征点调整至5000元,估计有50%的当地职工会被征税;③根据此次调查,为使60……以上的职工不用缴纳个人所得税,起征点应调^5200元其中正确结论的个数有( )
 A、0 B、1 C、2 D、36. 若双曲线的实轴长为 , 则该双曲线的渐近线方程为( )A、 B、 C、 D、7. 已知正四棱锥的高为2, , 过该棱锥高的中点且平行于底面的平面截该正四棱锥所得截面为A1B1C1D1 , 若底面与截面的顶点在同一球面上,则该球的表面积为( )A、20π B、 C、4π D、8. 已知函数 , 则方程的实根个数为( )个.A、1 B、2 C、3 D、49. 已知函数的图象如图所示,则等于( )
A、0 B、1 C、2 D、36. 若双曲线的实轴长为 , 则该双曲线的渐近线方程为( )A、 B、 C、 D、7. 已知正四棱锥的高为2, , 过该棱锥高的中点且平行于底面的平面截该正四棱锥所得截面为A1B1C1D1 , 若底面与截面的顶点在同一球面上,则该球的表面积为( )A、20π B、 C、4π D、8. 已知函数 , 则方程的实根个数为( )个.A、1 B、2 C、3 D、49. 已知函数的图象如图所示,则等于( )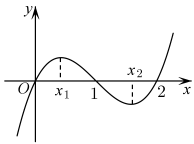 A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
10. 复数的虚部是.11. 圆 的圆心到直线 的距离为 ,则 .12. 随机变量 ,若 , ,则 .13. 计算: .14. 已知菱形的边长为4,是的中点,则 .15. 在(x2+ )8的展开式中,x7的系数为 . (用数字作答)
三、解答题
-
16. 在锐角中,内角 , , 的对边分别为 , , , 且(1)、求角的大小;(2)、若 , , 求 , .17. 如图,已知椭圆 , , 分别为椭圆的左、右焦点,为椭圆的上顶点,直线交椭圆于另一点.
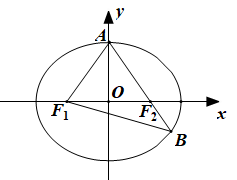 (1)、若 , 求椭圆的离心率;(2)、若椭圆的焦距为2,且 , 求椭圆的方程.
(1)、若 , 求椭圆的离心率;(2)、若椭圆的焦距为2,且 , 求椭圆的方程.
