天津市滨海七校2022届高三下学期数学二模试卷
试卷更新日期:2022-06-27 类型:高考模拟
一、单选题
-
1. 定义 , 若 , , 则A-B=( )A、{9} B、{0,3,7} C、{1,5} D、{0,1,3,5,7}2. “ 且 ”是“直线 过点 ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分又不必要条件3. 某班50名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].从样本成绩不低于80分的学生中随机选取2人,记这2人成绩在90分以上(含90分)的人数为ξ,则ξ的数学期望为( )
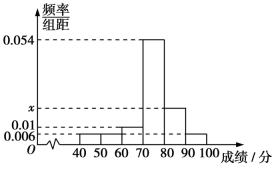 A、 B、 C、 D、4. 函数的图象大致为( )A、
A、 B、 C、 D、4. 函数的图象大致为( )A、 B、
B、 C、
C、 D、
D、 5. 设实数 满足 则 的大小关系为( )A、c<a<b B、c<b<a C、a<c<b D、b<c<a6. 已知三棱锥的底面是以为斜边的等腰直角三角形, , 设四点均在以为球心的某个球面上,则到平面的距离为( )A、 B、 C、 D、7. 唐代诗人李欣的是 古从军行 开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有趣的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为 ,若将军从 出发,河岸线所在直线方程 ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )A、 B、 C、 D、8. 已知函数图象相邻两条对称轴之间的距离为 , 将函数的图象向左平移个单位后,得到的图象关于轴对称,那么函数的图象( )A、关于点对称 B、关于点对称 C、关于直线对称 D、关于直线对称9. 已知函数 ( ,且 )在 上单调递减,且关于x的方程 恰有两个不相等的实数解,则 的取值范围是( )A、 B、[ , ] C、[ , ] { } D、[ , ) { }
5. 设实数 满足 则 的大小关系为( )A、c<a<b B、c<b<a C、a<c<b D、b<c<a6. 已知三棱锥的底面是以为斜边的等腰直角三角形, , 设四点均在以为球心的某个球面上,则到平面的距离为( )A、 B、 C、 D、7. 唐代诗人李欣的是 古从军行 开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有趣的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为 ,若将军从 出发,河岸线所在直线方程 ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )A、 B、 C、 D、8. 已知函数图象相邻两条对称轴之间的距离为 , 将函数的图象向左平移个单位后,得到的图象关于轴对称,那么函数的图象( )A、关于点对称 B、关于点对称 C、关于直线对称 D、关于直线对称9. 已知函数 ( ,且 )在 上单调递减,且关于x的方程 恰有两个不相等的实数解,则 的取值范围是( )A、 B、[ , ] C、[ , ] { } D、[ , ) { }二、填空题
-
10. 如果复数z满足 , 那么的最大值是 .11. 若 的展开式中x4的系数为7,则实数a= .12. 已知圆C:x2+y2+2x+ay-3=0(a为实数)上任意一点关于直线l:x-y+2=0的对称点都在圆C上,则a= .
13. 银行储蓄卡的密码由6位数字组成,某人在银行自助取款机上取钱时,忘记了密码的最后1位数字,如果记得密码的最后1位是偶数,则第2次按对的概率是.14. 已知ab= , a,b∈(0,1),则的最小值为 ,15. 如图直角梯形中, , , , 在等腰直角三角形中, , 则向量在向量上的投影向量的模为;若 , 分别为线段 , 上的动点,且 , 则的最小值为 .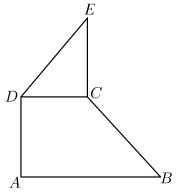
三、解答题
-
16. 设的内角A,B,C的对边分别为a,b,c, , 且(1)、求证:;(2)、若的面积为 , 求.17. 如图所示,在几何体ABCDEF中,四边形ABCD为直角梯形,AD∥BC,AB⊥AD,AE⊥底面ABCD,AE∥CF,AD=3,AB=BC=AE=2,CF=1.
 (1)、求证:BF∥平面ADE;(2)、求直线BE与直线DF所成角的余弦值;(3)、求点D到直线BF的距离.
(1)、求证:BF∥平面ADE;(2)、求直线BE与直线DF所成角的余弦值;(3)、求点D到直线BF的距离.
