北京市朝阳区2022届高三数学二模试卷

试卷更新日期：2022-06-27 类型：高考模拟

进入出卷网下载

一、单选题

1. 集合 $A = {1 ， 2 ， 3 ， 4} ， B = {x | x > 2}$ ，则 $A ∩ B =$ （）

A、 ${1 ， 2}$ B、 ${3 ， 4}$ C、 ${2 ， 3 ， 4}$ D、 ${1 ， 2 ， 3 ， 4}$

查看试题解析
2. 在复平面内，复数 $\frac{i}{1 - i}$ 对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - y^{2} = 1 (a > 0)$ 的一条渐近线方程为 $y = x$ ，则C的离心率为（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

查看试题解析
4. 已知角 $α$ 的终边经过点 $P (- \frac{3}{5} ， \frac{4}{5})$ ，则 $s i n 2 α =$ （）

A、 $- \frac{24}{25}$ B、 $- \frac{7}{25}$ C、 $\frac{7}{25}$ D、 $\frac{24}{25}$

查看试题解析
5. 过点 $(1 ， 2)$ 作圆 $x^{2} + y^{2} = 5$ 的切线，则切线方程为（）

A、 $x = 1$ B、 $3 x - 4 y + 5 = 0$ C、 $x + 2 y - 5 = 0$ D、 $x = 1$ 或 $x + 2 y - 5 = 0$

查看试题解析
6. “ $m > n > 0$ ”是“ $(m - n) (l o g_{2} m - l o g_{2} n) > 0$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
7. 已知l，m是两条不同的直线， $α ， β$ 是两个不同的平面，下面正确的结论是（）

A、若 $l / / α ， m / / α$ ，则 $l / / m$ B、若 $m / / β ， α ⊥ β$ ，则 $m ⊥ α$ C、若 $l ⊥ α ， l ⊥ m$ ，则 $m / / α$ D、若 $l ⊥ β ， m ⊥ β ， m ⊥ α$ ，则 $l ⊥ α$

查看试题解析
8. ISO216是国际标准化组织所定义的纸张尺寸国际标准，该标准定义了A，B系列的纸张尺寸．设型号为 $A 0 ， A 1 ， A 2 ， A 3 ， A 4 ， A 5 ， A 6$ 的纸张的面积分别是 $a_{0} ， a_{1} ， a_{2} ， a_{3} ， a_{4} ， a_{5} ， a_{6}$ ，它们组成一个公比为 $\frac{1}{2}$ 的等比数列，设型号为 $B 1 ， B 2 ， B 3 ， B 4 ， B 5 ， B 6$ 的纸张的面积分别是 $b_{1} ， b_{2} ， b_{3} ， b_{4} ， b_{5} ， b_{6}$ 已知 $b_{i}^{2} = a_{i - 1} a_{i} (i = 1 ， 2 ， 3 ， 4 ， 5 ， 6)$ ，则 $\frac{a_{4}}{b_{5}}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、2

查看试题解析
9. 已知M为 $△ A B C$ 所在平面内的一点， $| \vec{M B} | = | \vec{M C} | = 1$ ，且 $\vec{A B} = \vec{M B} + \vec{M C} ， \vec{M B} \cdot \vec{M C} = - \frac{1}{2}$ ，则 $\vec{C A} \cdot \vec{C B} =$ （）

A、0 B、1 C、 $\sqrt{3}$ D、3

查看试题解析
10. 某工厂产生的废气经过滤后排放，过滤过程中废气的污染物含量P（单位： $m g / L$ ）与时间t（单位：h）间的关系为 $P = P_{0} e^{- k t}$ ，其中 $P_{0}$ ， k是正的常数．如果在前 $10 h$ 污染物减少19%，那么再过 $5 h$ 后污染物还剩余（）

A、40.5% B、54% C、65.6% D、72.9%

查看试题解析

二、填空题

11. 抛物线 $y^{2} = 4 x$ 的准线方程是

查看试题解析
12. 在 $(x + \sqrt{x})^{5}$ 的展开式中， $x^{3}$ 的系数是．（用数字作答）

查看试题解析
13. 已知 $△ A B C$ 的三个角A，B，C的对边分别为a，b，c，则能使 $\frac{c o s A}{c o s B} = \frac{b}{a}$ 成立的一组A，B的值是．

查看试题解析
14. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ ，中，E，F，G分别为棱 $A_{1} A ， A_{1} B_{1} ， A_{1} D_{1}$ 上的点（与正方体顶点不重合），过 $A_{1}$ 作 $A_{1} H ⊥$ 平面 $E F G$ ，垂足为H．设正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，给出以下四个结论：
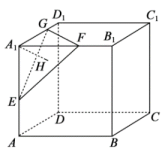
①若E，F，G分别是 $A_{1} A ， A_{1} B_{1} ， A_{1} D_{1}$ 的中点，则 $A_{1} H = \frac{\sqrt{3}}{6}$ ；
②若E，F，G分别是 $A_{1} A ， A_{1} B_{1} ， A_{1} D_{1}$ 的中点，则用平行于平面 $E F G$ 的平面去截正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ ，得到的截面图形一定是等边三角形；
③ $△ E F G$ 可能为直角三角形；
④ $\frac{1}{A_{1} E^{2}} + \frac{1}{A_{1} F^{2}} + \frac{1}{A_{1} G^{2}} = \frac{1}{A_{1} H^{2}}$ ．
其中所有正确结论的序号是．

查看试题解析
15. “杨辉三角”是数学史上的一个伟大成就．在如图所示的“杨辉三角”中，去掉所有的数字1，余下的数逐行从左到右排列，得到数列 ${a_{n}}$ 为2，3，3，4，6，4，5，10，…，则数列 ${a_{n}}$ 的前10项和为；若 $a_{m} = 10 ， m \in N^{*}$ ，则m的最大值为．
$\begin{array}{l} 1 \\ 1 1 \\ 1 2 1 \\ 1 3 3 1 \\ 1 4 6 4 1 \\ 1 5 10 10 5 1 \\ 1 6 15 20 15 6 1 \\ ⋮ \end{array}$

查看试题解析

三、解答题

16. 已知函数 $f (x) = c o s^{2} ω x + \sqrt{3} s i n ω x c o s ω x + m (ω > 0 ， m \in R)$ ．再从条件①、条件②、条件③这三个条件中选择能确定函数 $f (x)$ 的解析式的两个作为已知．

(1)、求 $f (x)$ 的解析式及最小值；

(2)、若函数 $f (x)$ 在区间 $[0 ， t] (t > 0)$ 上有且仅有1个零点，求t的取值范围．
条件①：函数 $f (x)$ 的最小正周期为 $π$ ；
条件②：函数 $f (x)$ 的图象经过点 $(0 ， \frac{1}{2})$ ；
条件③：函数 $f (x)$ 的最大值为 $\frac{3}{2}$ ．
注：如果选择的条件不符合要求，得0分；如果选择多组符合要求的条件分别解答，按第一组解答计分．

查看试题解析
17. 如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，底面 $A B C D$ 是边长为2的正方形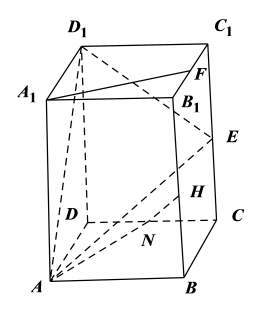， $D D_{1} = 4$ ， E，F分别是 $C C_{1} ， B_{1} C_{1}$ 的中点．

(1)、求证： $A_{1} F$ ∥平面 $A E D_{1}$ ；

(2)、设H在棱 $B B_{1}$ 上，且 $B H = \frac{1}{4} B B_{1}$ ， N为 $C D$ 的中点，求证： $N H ⊥$ 平面 $A E D_{1}$ ；并求直线 $A N$ 与平面 $A E D_{1}$ 所成角的正弦值．

查看试题解析
18. 为实现乡村的全面振兴，某地区依托乡村特色优势资源，鼓励当地农民种植中药材，批发销售．根据前期分析多年数据发现，某品种中药材在该地区各年的平均每亩种植成本为5000元，此品种中药材在该地区各年的平均每亩产量与此品种中药材的国内市场批发价格均具有随机性，且互不影响，其具体情况如下表：
该地区此品种中药材各年的平均每亩产量情况
各年的平均每亩产量
$400 k g$
$500 k g$
频率
0.25
0.75
（注：各年的平均每亩纯收入=各年的平均每亩产量×批发价格-各年的平均每亩种植成本）

(1)、以频率估计概率，试估计该地区某农民2022年种植此品种中药材获得最高纯收入的概率；

(2)、设该地区某农民2022年种植此品种中药材的平均每亩纯收入为X元，以频率估计概率，求X的分布列和数学期望；

(3)、已知该地区某农民有一块土地共10亩，该块土地现种植其他农作物，年纯收入最高可达到45000元，根据以上数据，该农民下一年是否应该选择在这块土地种植此品种中药材？说明理由．

查看试题解析
19. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的一个顶点为 $P (0 ， 1)$ ，离心率为 $\frac{\sqrt{2}}{2}$ ．

(1)、求椭圆 $C$ 的方程；

(2)、过点 $P$ 作斜率为 $k_{1}$ 的直线 $l_{1}$ 交椭圆 $C$ 于另一点 $A$ ，过点 $P$ 作斜率为 $k_{2} (k_{2} \neq k_{1})$ 的直线 $l_{2}$ 交椭圆 $C$ 于另一点 $B$ ．若 $k_{1} k_{2} = 1$ ，求证：直线 $A B$ 经过定点．

查看试题解析
20. 已知函数 $f (x) = x s i n x + c o s x$ ．

(1)、当 $x \in (0 ， π)$ 时，求函数 $f (x)$ 的单调区间；

(2)、设函数 $g (x) = - x^{2} + 2 a x$ ．若对任意 $x_{1} \in [- π ， π]$ ，存在 $x_{2} \in [0 ， 1]$ ，使得 $\frac{1}{2 π} f (x_{1}) \leq g (x_{2})$ 成立，求实数a的取值范围．

查看试题解析
21. 已知集合 $A = {α | α = (x_{1} ， x_{2} ， x_{3} ， x_{4}) ， x_{i} \in N ， i = 1 ， 2 ， 3 ， 4}$ ．对集合A中的任意元素 $α = (x_{1} ， x_{2} ， x_{3} ， x_{4})$ ，定义 $T (α) = (| x_{1} - x_{2} | ， | x_{2} - x_{3} | ， | x_{3} - x_{4} | ， | x_{4} - x_{1} |)$ ，当正整数 $n \geq 2$ 时，定义 $T^{n} (α) = T (T^{n - 1} (α))$ （约定 $T^{1} (α) = T (α)$ ）．

(1)、若 $α = (2 ， 0 ， 2 ， 1) ， β = (2 ， 0 ， 2 ， 2)$ ，求 $T^{4} (α)$ 和 $T^{4} (β)$ ；

(2)、若 $α = (x_{1} ， x_{2} ， x_{3} ， x_{4})$ 满足 $x_{i} \in {0 ， 1} (i = 1 ， 2 ， 3 ， 4)$ 且 $T^{2} (α) = (1 ， 1 ， 1 ， 1)$ ，求 $α$ 的所有可能结果；

(3)、是否存在正整数n使得对任意 $α = (x_{1} ， x_{2} ， x_{3} ， x_{4}) \in A (x_{1} \geq x_{2} \geq x_{4} \geq x_{3})$ 都有 $T^{n} (α) = (0 ， 0 ， 0 ， 0)$ ？若存在，求出n的所有取值；若不存在，说明理由．

查看试题解析

各年的平均每亩产量	$400 k g$	$500 k g$
频率	0.25	0.75